（本小题共13分）某厂生产的产品在出厂前都要做质量检测，每一件一等品都能通过检测，每一件二等品通过检测的概率为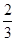
．现有10件产品，其中6件是一等品，4件是二等品．
（Ⅰ） 随机选取1件产品，求能够通过检测的概率；
（Ⅱ） 随机选取3件产品，其中一等品的件数记为
，求的分布列；
（Ⅲ） 随机选取3件产品，求这三件产品都不能通过检测的概率．
（本小题满分10分）.
写出命题
，则x = 2且y= 一1”的逆命题、否命题、逆否命题，并判断真假．
（本小题满分12分）
如图，斜率为1的直线过抛物线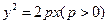
的焦点，与抛物线交于两点A、B，将直线AB按向量
平移得直线
，N为上的动点。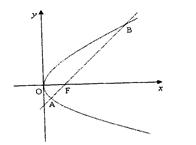
（1）若|AB|=8，求抛物线的方程；
（2）求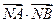
的最小值。
（本小题满分12分）
已知函数
（1）求函数的单调区间；
（2）a为何值时，方程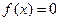
有三个不同的实根。
（本小题满分13分）
如图，SD垂直于正方形ABCD所在的平面，AB=1，
（1）求证：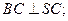
（2）设棱SA的中点为M，求异面直线DM与SC所成角的大小。
（本小题满分13分）
如图是两个独立的转盘（A）、（B），在两个图中三个扇形区域的圆心角分别为
，用这两个转盘进行游戏，规则是：同时转动两个转盘待指针停下（当两个转盘中任意一个指针恰好落在分界线时，则这次转动无效，重新开始），记转盘（A）指针所对的区域为x，转盘（B）指针所对的区域为y，
，设
的值为
（1）求
的概率；
（2）求随机变量
的发布列与数学期望。