已知椭圆 :
: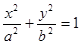
 ,
,
(1)若椭圆的长轴长为4,离心率为 ,求椭圆的标准方程;
,求椭圆的标准方程;
(2)在(1)的条件下,设过定点 的直线
的直线 与椭圆
与椭圆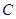 交于不同的两点
交于不同的两点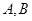 ,且
,且 为锐角(
为锐角(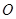 为坐标原点),求直线
为坐标原点),求直线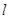 的斜率
的斜率 的取值范围;
的取值范围;
(3)过原点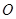 任意作两条互相垂直的直线与椭圆
任意作两条互相垂直的直线与椭圆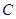 :
: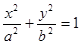
 相交于
相交于 四点,设原点
四点,设原点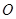 到四边形
到四边形 的一边距离为
的一边距离为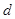 ,试求
,试求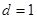 时
时 满足的条件.
满足的条件.
设A={x|x2+4x=0},B={x|x2+2(a+1)x+a2-1=0},其中x∈R,如果A∩B=B,求实数a的取值范围.
设集合A为函数y=ln(-x2-2x+8)的定义域,集合B为函数y=x+的值域.求A∩B
设曲线 在点
在点 处的切线斜率为
处的切线斜率为 ,且
,且 .对一切实数
.对一切实数 ,不等式
,不等式 恒成立(
恒成立( ≠0).
≠0).
(1) 求 的值;
的值;
(2) 求函数 的表达式;
的表达式;
(3) 求证: >
> .
.
已知函数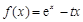 (e为自然对数的底数).
(e为自然对数的底数).
(1)求函数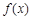 的单调增区间;
的单调增区间;
(2)设关于x的不等式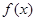 ≥
≥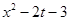 的解集为M,且集合
的解集为M,且集合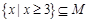 ,求实数t的取值范围.
,求实数t的取值范围.
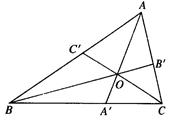
已知 是
是 内任意一点,连结
内任意一点,连结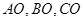 并延长交对边于
并延长交对边于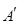 ,
, ,
,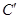 ,则
,则 .这是平面几何的一个命题,其证明常常采用“面积法”:
.这是平面几何的一个命题,其证明常常采用“面积法”:  .
.
运用类比,猜想对于空间中的四面体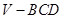 ,存在什么类似的结论,并用“体积法”证明.
,存在什么类似的结论,并用“体积法”证明.