已知数列{ }中,
}中, ,且
,且 对任意正整数都成立,数列{
对任意正整数都成立,数列{ }的前n项和为
}的前n项和为
(1)若 ,且
,且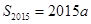 ,求a;
,求a;
(2)是否存在实数k,使数列{ }是公比不为1的等比数列,且任意相邻三项
}是公比不为1的等比数列,且任意相邻三项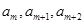 按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
(3)若 .
.
已知函数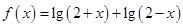 .
.
(1)求函数 的定义域;
的定义域;
(2)若不等式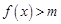 有解,求实数
有解,求实数 的取值范围.
的取值范围.
设全集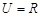 ,
,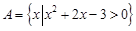 ,
,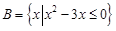 .求:
.求:
(1)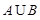 ;(2)
;(2) .
.
已知函数
 在
在 处取得极值
处取得极值 ,其中
,其中 为常数.
为常数.
(1)求 的值;
的值;
(2)讨论函数 的单调区间;
的单调区间;
(3)若对任意 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
如图,已知⊙ 与⊙
与⊙ 外切于点
外切于点 ,
, 是两圆的外公切线,
是两圆的外公切线, ,
, 为切点,
为切点, 与
与 的延长线相交于点
的延长线相交于点 ,延长
,延长 交⊙
交⊙ 于 点
于 点 ,点
,点 在
在 延长线上.
延长线上.
(1)求证: 是直角三角形;
是直角三角形;
(2)若 ,试判断
,试判断 与
与 能否一定垂直?并说明理由.
能否一定垂直?并说明理由.
(3)在(2)的条件下,若 ,
, ,求
,求 的值.
的值.
设在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片,标号分别记为 ,设随机变量
,设随机变量 .
.
(1)写出 的可能取值,并求随机变量
的可能取值,并求随机变量 的最大值;
的最大值;
(2)求事件“ 取得最大值”的概率;
取得最大值”的概率;
(3)求 的分布列和数学期望与方差.
的分布列和数学期望与方差.