如图所示,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点, PA=PD=4,BC=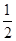 AD=2,CD=
AD=2,CD= .
.
(Ⅰ)求证:PA⊥CD;
(Ⅱ)若M是棱PC的中点,求直线PB与平面BEM所成角的正弦值;
(Ⅲ)在棱PC上是否存在点N,使二面角N-EB-C的余弦值为 ,若存在,确定点N的位置;若不存在,请说明理由.
,若存在,确定点N的位置;若不存在,请说明理由.
(本小题满分10分)
已知向量m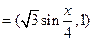 ,n
,n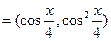 ,函数
,函数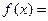 m·n.
m·n.
(Ⅰ)若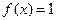 ,求
,求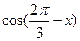 的值;
的值;
(Ⅱ)在锐角△ABC中,角A,B,C的对边分别是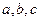 ,且满足
,且满足 ,求
,求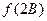
的取值范围。
(本小题满分12分)
设函数f(x)=x3+ax2+bx(x>0)的图象与直线y=4相切于M(1,4).
(Ⅰ)求f(x)=x3+ax2+bx在区间(0,4]上的最大值与 最小值;
最小值;
(Ⅱ)设存在两个不等正数s,t(s<t),当x∈[s,t]时,函数f(x)=x3+ax2+bx的值域是[ks,kt],求正数k的取值范围。
(本小题满分12分)
已知动圆P过点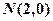 并且与圆
并且与圆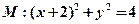 相外切,动圆圆心P的轨迹为W,过点N的直线
相外切,动圆圆心P的轨迹为W,过点N的直线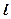 与轨迹W交于A、B两点。
与轨迹W交于A、B两点。
(Ⅰ)求轨迹W的方程;(Ⅱ)若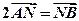 ,求直线
,求直线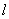 的方程;
的方程;
(Ⅲ)对于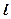 的任意一确定的位置,在直线
的任意一确定的位置,在直线 上是否存在一点Q,使得
上是否存在一点Q,使得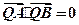 ,并说明理由。
,并说明理由。
(本小题满分12分)
已知数列 满足
满足 (t>0,n≥2),且
(t>0,n≥2),且 ,n≥2时,
,n≥2时, >0.其中
>0.其中 是数列
是数列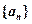 的前n项和.
的前n项和.
(Ⅰ)求数列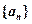 的通项公式;
的通项公式;
(Ⅱ)若对于 ,不等式
,不等式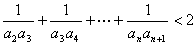 恒成立,求t 的取值范围.
恒成立,求t 的取值范围.
(本小题满分12分)
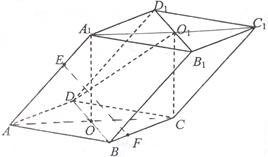
已知平行六面体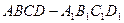 的底面为正方形,
的底面为正方形,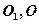 分别为上、下底面的中心,且
分别为上、下底面的中心,且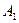 在底面
在底面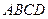 的射影是
的射影是 。
。 (Ⅰ)求证:平面
(Ⅰ)求证:平面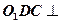 平面
平面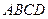 ;
;
(Ⅱ)若点 分别在棱上
分别在棱上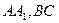 上,且
上,且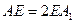 ,问点
,问点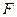 在何处时,
在何处时,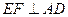 ;
;
(Ⅲ)若 ,求二面角
,求二面角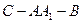 的大小(用反三角函数表示)。
的大小(用反三角函数表示)。