(本小题满分12分)
已知平行六面体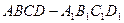 的底面为正方形,
的底面为正方形,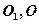 分别为上、下底面的中心,且
分别为上、下底面的中心,且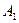 在底面
在底面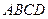 的射影是
的射影是 。
。 (Ⅰ)求证:平面
(Ⅰ)求证:平面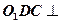 平面
平面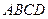 ;
;
(Ⅱ)若点 分别在棱上
分别在棱上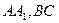 上,且
上,且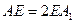 ,问点
,问点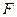 在何处时,
在何处时,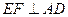 ;
;
(Ⅲ)若 ,求二面角
,求二面角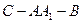 的大小(用反三角函数表示)。
的大小(用反三角函数表示)。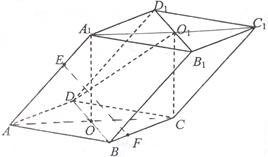
已知x=1是函数f(x)=mx3-3(m+1)x2+nx+1的一个极值点,其中m,n∈R.
(1)求m与n的关系式;
(2)求f(x)的单调区间;
(3)当x∈[-1,1]时,m<0,函数y=f(x)的图象上任意一点的切线斜率恒大于3m,求m的取值范围.
(用数字表示结果)
某校举行环保知识大奖赛,比赛分初赛和决赛两部分,初赛采用选一题答一题的方式进行。每位选手最多有5次答题机会。选手累计答对3题或答错三题终止初赛的比赛。答对三题直接进入决赛,答错3题则被淘汰。已知选手甲连续两次答错的概率为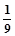 (已知甲回答每个问题的正确率相同,并且相互之间没有影响)
(已知甲回答每个问题的正确率相同,并且相互之间没有影响)
(1)求选手甲回答一个问题的正确率;
(2)求选手甲进入决赛的概率;
(3)设选手甲在初赛中答题个数为X,试写出X的分布列,并求甲在初赛中平均答题个数。
已知数列{an}满足a1= ,且前n项和Sn满足:Sn=n2an,求a2,a3,a4,猜想{an}的通项公式,并加以证明。
,且前n项和Sn满足:Sn=n2an,求a2,a3,a4,猜想{an}的通项公式,并加以证明。
已知a>0,求证: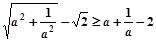
12分)
要从两名同学中挑出一名,代表班级参加射击比赛,根据以往的成绩记录同学甲击中目标的环数为X1的分布列为
| X1 |
5 |
6 |
7 |
8 |
9 |
10 |
| P |
0.03 |
0.09 |
0.20 |
0.31 |
0.27 |
0.10 |
同学乙击目标的环数X2的分布列为
| X2 |
5 |
6 |
7 |
8 |
9 |
| P |
0.01 |
0.05 |
0.20 |
0.41 |
0.33 |
(1)请你评价两位同学的射击水平(用数据作依据);
(2)如果其它班参加选手成绩都在9环左右,本班应派哪一位选手参赛,如果其它班参赛选手的成绩都在7环左右呢?