12分)
要从两名同学中挑出一名,代表班级参加射击比赛,根据以往的成绩记录同学甲击中目标的环数为X1的分布列为
| X1 |
5 |
6 |
7 |
8 |
9 |
10 |
| P |
0.03 |
0.09 |
0.20 |
0.31 |
0.27 |
0.10 |
同学乙击目标的环数X2的分布列为
| X2 |
5 |
6 |
7 |
8 |
9 |
| P |
0.01 |
0.05 |
0.20 |
0.41 |
0.33 |
(1)请你评价两位同学的射击水平(用数据作依据);
(2)如果其它班参加选手成绩都在9环左右,本班应派哪一位选手参赛,如果其它班参赛选手的成绩都在7环左右呢?
对定义在区间l,上的函数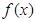 ,若存在开区间
,若存在开区间 和常数C,使得对任意的
和常数C,使得对任意的 都有
都有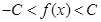 ,且对任意的x
,且对任意的x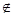 (a,b)都有
(a,b)都有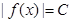 恒成立,则称函数
恒成立,则称函数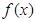 为区间I上的“Z型”函数.
为区间I上的“Z型”函数.
(I)求证:函数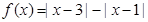 是R上的“Z型”函数;
是R上的“Z型”函数;
(Ⅱ)设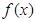 是(I)中的“Z型”函数,若不等式
是(I)中的“Z型”函数,若不等式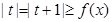 对任意的x
对任意的x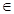 R恒成立,求实数t的取值范围.
R恒成立,求实数t的取值范围.
在平面直角坐标系xOy中,已知圆锥曲线C的参数方程为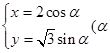 为参数).
为参数).
(I)以原点为极点,x轴正半轴为极轴建立极坐标系,求圆锥曲线C的极坐标方程;
(Ⅱ)若直线l过曲线C的焦点且倾斜角为60°,求直线l被圆锥曲线C所截得的线段的长度.
如图,过半径为4的⊙O上的一点A引半径为3的⊙O′的切线,切点为B,若⊙O与⊙O′内切于点M,连接AM与⊙O′交于c点,求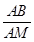 的值.
的值.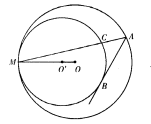
定义:已知函数f(x)与g(x),若存在一条直线y="kx" +b,使得对公共定义域内的任意实数均满足g(x)≤f(x)≤kx+b恒成立,其中等号在公共点处成立,则称直线y="kx" +b为曲线f(x)与g(x)的“左同旁切线”.已知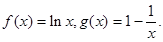
(I)证明:直线y=x-l是f(x)与g(x)的“左同旁切线”;
(Ⅱ)设P(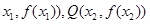 是函数 f(x)图象上任意两点,且0<x1<x2,若存在实数x3>0,使得
是函数 f(x)图象上任意两点,且0<x1<x2,若存在实数x3>0,使得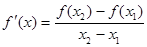 .请结合(I)中的结论证明:
.请结合(I)中的结论证明: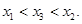
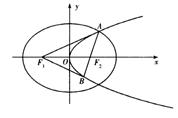
椭圆M的中心在坐标原点D,左、右焦点F1,F2在x轴上,抛物线N的顶点也在原点D,焦点为F2,椭圆M与抛物线N的一个交点为A(3, ).
).
(I)求椭圆M与抛物线N的方程;
(Ⅱ)在抛物线N位于椭圆内(不含边界)的一段曲线上,是否存在点B,使得△AF1B的外接圆圆心在x轴上?若存在,求出B点坐标;若不存在,请说明理由.