某中学有甲乙两个文科班进行数学考试，按照大于或等于120分为优秀，120分以下为非优秀统计成绩后，得到如下列联表：
| |
优秀 |
非优秀 |
合计 |
| 甲 |
20 |
5 |
25 |
| 乙 |
10 |
15 |
25 |
| 合计 |
30 |
20 |
50 |
（Ⅰ）用分层抽样的方法在优秀的学生中抽6人，其中甲班抽多少人？
（Ⅱ）在上述抽取的6人中选2人，求恰有一名同学在乙班的概率；
（Ⅲ）计算出统计量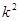
，若按95%可靠性要求能否认为“成绩与班级有关”．
下面的临界值表代参考：
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
（参考公式
其中
）
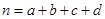如图,在侧棱垂直底面的四棱柱ABCD
A1B1C1D1中,AD∥BC,AD⊥AB,AB=
,AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E与直线AA1的交点.
(1)证明:①EF∥A1D1;②BA1⊥平面B1C1EF.
(2)求BC1与平面B1C1EF所成的角的正弦值.
如图所示,已知两个正方形ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.
(1)若CD=2,平面ABCD⊥平面DCEF,求MN的长;
(2)用反证法证明:直线ME与BN是两条异面直线.
正实数数列{an}中,a1=1,a2=5,且{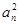
}成等差数列.
(1)证明:数列{an}中有无穷多项为无理数;
(2)当n为何值时,an为整数?并求出使an<200的所有整数项的和.
已知函数f(x)=(x-a)2(x-b)(a,b∈R,a<b).
(1)当a=1,b=2时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)设x1,x2是f(x)的两个极值点,x3是f(x)的一个零点,且x3≠x1,x3≠x2.证明:存在实数x4,使得x1,x2,x3,x4按某种顺序排列后构成等差数列,并求x4.
如图,已知△ABC中的两条角平分线AD和CE相交于H,∠B=60°,F在AC上,且AE=AF.
(1)证明:B,D,H,E四点共圆;
(2)证明:CE平分∠DEF.