新建的荆州中学拟模仿图甲建造一座体育馆,其设计方案侧面的外轮廓线如图乙所示:曲线 是以点
是以点 为圆心的圆的一部分,其中
为圆心的圆的一部分,其中 单位:米
单位:米 ;曲线
;曲线 是抛物线
是抛物线 的一部分;
的一部分; ,且
,且 恰好等于圆
恰好等于圆 的半径.假定拟建体育馆的高
的半径.假定拟建体育馆的高 米.
米.
(Ⅰ)若要求 米,
米,  米,求
米,求 与
与 的值;
的值;
(Ⅱ)若 ,将
,将 的长表示为点
的长表示为点 的纵坐标
的纵坐标 的函数
的函数 ,并求
,并求 的最大值.
的最大值.
并求 的最大值.(参考公式:若
的最大值.(参考公式:若 ,则
,则 ,其中
,其中 为常数)
为常数)
阅读下面材料:
根据两角和与差的正弦公式,有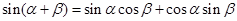 ------①
------①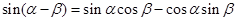 ------②
------②
由①+② 得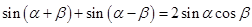 ------③
------③
令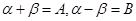 有
有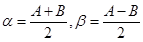
代入③得 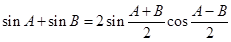
(Ⅰ)类比上述推证方法,根据两角和与差的余弦公式,证明: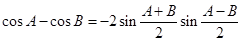 ;
;
(Ⅱ)若 的三个内角
的三个内角 满足
满足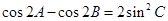 ,试判断
,试判断 的形状.
的形状.
(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
函数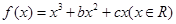 ,已知
,已知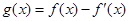 是奇函数。
是奇函数。
(Ⅰ)求b,c的值;
(Ⅱ)求g(x)的单调区间与极值。
如图,已知点D(0,-2),过点D作抛物线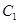 :
: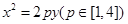 的切线
的切线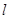 ,切点A在第二象限。
,切点A在第二象限。
(1)求切点A的纵坐标;
(2)若离心率为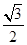 的椭圆
的椭圆 恰好经过A点,设切线l交椭圆的另一点为B,若设切线
恰好经过A点,设切线l交椭圆的另一点为B,若设切线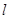 ,直线OA,OB的斜率为
,直线OA,OB的斜率为 ,
,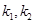 ,①试用斜率k表示
,①试用斜率k表示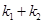 ②当
②当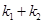 取得最大值时求此时椭圆的方程。
取得最大值时求此时椭圆的方程。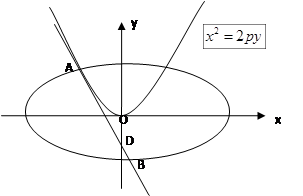
已知函数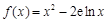 .(
.(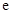 为自然对数的底)
为自然对数的底)
(Ⅰ)求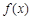 的最小值;
的最小值;
(Ⅱ)是否存在常数 使得
使得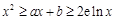 对于任意的正数
对于任意的正数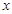 恒成立?若存在,求出
恒成立?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
已知椭圆的方程为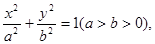 它的一个焦点与抛物线
它的一个焦点与抛物线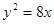 的焦点重合,离心率
的焦点重合,离心率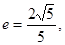 过椭圆的右焦点F作与坐标轴不垂直的直线
过椭圆的右焦点F作与坐标轴不垂直的直线 交椭圆于A、B两点.(Ⅰ)求椭圆的标准方程;
交椭圆于A、B两点.(Ⅰ)求椭圆的标准方程;
(Ⅱ)设点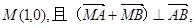 求直线
求直线 的方程
的方程