（本小题满分14分）已知函数f（x）=x2e-2ax（a＞0），
（1）已知函数f（x）的曲线在x＝1处的切线方程为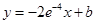
，求实数
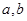的值；
（2）求函数在［1，2］上的最大值．
如图，将边长为2，有一个锐角为60°的菱形
，沿着较短的对角线
对折，使得
，
为的中点.
（Ⅰ）求证：
（Ⅱ）求三棱锥
的体积；
（Ⅲ）求二面角
的余弦值.
已知点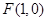
，直线
，动点
到点
的距离等于它到直线
的距离.
（Ⅰ）求点的轨迹
的方程；
（Ⅱ）是否存在过
的直线
，使得直线被曲线截得的弦
恰好被点
所平分？
已知函数
在点
处的切线方程为
.
（Ⅰ）求
的值；
（Ⅱ）求
的单调区间.
已知函数f（x）的定义域为
，且满足f（2）=1，f（xy）＝f（x）+f（y），
（1）求f（1），f（4）， f（8）的值；
（2）函数f（x）当
时都有
.若
成立，求
的取值范围．
运货卡车以每小时x千米的速度匀速行驶120千米（50≤x≤100）（单位：千米/小时）．假设汽油的价格是每升2元，而汽车每小时耗油
升，司机的工资是每小时12元．
（1）求这次行车总费用y关于x的表达式；
（2）当x为何值时，这次行车的总费用最低，并求出最低费用的值．