已知函数f(x)的定义域为 ,且满足f(2)=1,f(xy)=f(x)+f(y),
,且满足f(2)=1,f(xy)=f(x)+f(y),
(1)求f(1),f(4), f(8)的值;
(2)函数f(x)当 时都有
时都有 .若
.若 成立,求
成立,求 的取值范围.
的取值范围.
(本小题满分12分)已知
 .
.
(Ⅰ)当 时,求
时,求 的极值;
的极值;
(Ⅱ)当 时,
时, ≥0,求正数a的取值范围.
≥0,求正数a的取值范围.
(本小题满分12分)已知F1、F2是椭圆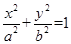 的左右焦点,离心率为
的左右焦点,离心率为 ,D是上顶点,C是右顶点,△CDF2的面积
,D是上顶点,C是右顶点,△CDF2的面积 .
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)若动直线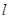 与椭圆E相交于A、B求△AOB面积的最大值.
与椭圆E相交于A、B求△AOB面积的最大值.
(本小题满分12分)某校在一次对是否喜欢英语学科的学生的抽样调查中,随机抽取了100名同学,相关的数据如下表所示:
| 不喜欢英语 |
喜欢英语 |
总计 |
|
| 男生 |
40 |
18 |
58 |
| 女生 |
15 |
27 |
42 |
| 总计 |
55 |
45 |
100 |
(Ⅰ)试运用独立性检验的思想方法分析:是否有99 %的把握认为“学生是否喜欢英语与性别有关?”说明理由.
(Ⅱ)用分层抽样方法在喜欢英语学科的学生中随机抽取5名,女学生应该抽取几名?
(Ⅲ)在上述抽取的5名学生中任取2名,求恰有1名学生为男性的概率.
附: =
= ,
,
 |
0.100 |
0.050 |
0.025 |
0.01 |
0.001 |
 |
2.706 |
3.841 |
5.024 |
6.635 |
10.828 |
(本小题满分12分)如图所示,直角梯形 与等腰直角
与等腰直角 所在平面互相垂直,
所在平面互相垂直, 为
为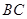 的中点,
的中点, ,
, ∥
∥ ,
, .
.
(Ⅰ)求证:平面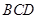
 平面
平面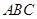 ;
;
(Ⅱ)求证: ∥平面
∥平面 ;
;
(Ⅲ)求四面体 的体积.
的体积.
(本大题满分12分)在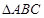 中,角
中,角 的对边分别为
的对边分别为 ,
, =
= ,
, =
= ,
, ∥
∥ .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若 ,且
,且 ,求
,求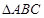 的面积.
的面积.