(本小题满分12分)已知F1、F2是椭圆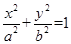 的左右焦点,离心率为
的左右焦点,离心率为 ,D是上顶点,C是右顶点,△CDF2的面积
,D是上顶点,C是右顶点,△CDF2的面积 .
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)若动直线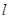 与椭圆E相交于A、B求△AOB面积的最大值.
与椭圆E相交于A、B求△AOB面积的最大值.
(本小题满分12分)
某校高三一次月考之后,为了了解数学学科的学习情况,现从中随机抽出若干名学生此次的数学成绩,按成绩分组,制成右面频率分布表:
(1)若每组数据用该组区间的中点值(例如区间[90,100)的中点值是95)作为代表,试估计该校高三学生本次月考的平均分;
(2)如果把表中的频率近似地看作每个学生在这次考试中取得相应成绩的概率,那么从所有学生中采用逐个抽取的方法任意抽取3名学生的成绩,并记成绩落在[110,130)中的学生数为ξ,求:
①在三次抽取过程 中至少有两次连续抽中成绩在[110,130)
中至少有两次连续抽中成绩在[110,130) 中的概率;
中的概率;
②ξ的分布列和数学期望.(注:本小题结果可用分数表示)
(本小题满分12分)
已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,
AB=BC=2CD,PO⊥平面ABCD.
(1)求证:BD⊥PE;
(2)若AO=2PO,求二面角D-PE-B的余弦值.
(本小题满分12分)
设数列{ }的前n项和
}的前n项和 满足:
满足: =n
=n -2n(n-1).等比数列{
-2n(n-1).等比数列{ }的前n项和为
}的前n项和为 ,公比为
,公比为
 ,且
,且 =
= +2
+2 .
.
(1)求数列{ }的通项公式;
}的通项公式;
(2)设数列{ }的前n项和为
}的前n项和为 ,求证:
,求证: ≤
≤ <
< .
.
(12分)已知函数 在
在 上是增函数,
上是增函数, 在
在 上为减函数。
上为减函数。
(1)求f(x) ,g(x)的解析式;
(2)求证:当x>0时,方程f( x)=g(x)+2有唯一解。
x)=g(x)+2有唯一解。
(12分)设函数 满足条件f(-1+x)=f(-1-x),且关于x的不等式
满足条件f(-1+x)=f(-1-x),且关于x的不等式 的解集为
的解集为
(1)求函数f(x)的解析式;
(2)若 时,不等式
时,不等式 恒成立,求实数t的取值范围。
恒成立,求实数t的取值范围。