为调查乘客的候车情况,公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间(单位:分钟)作为样本分成5组,如表所示:
| 组别 |
候车时间 |
人数 |
| 一 |
[0,5) |
2 |
| 二 |
[5,10) |
6 |
| 三 |
[10,15) |
4 |
| 四 |
[15,20) |
2 |
| 五 |
[20,25) |
1 |
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
(本题满分12分)
已知集合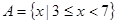 ,
,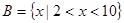 ,
,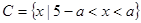 .
.
(1)求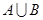 ,
, 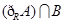 ;
;
(2)若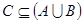 ,求
,求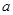 的取值范围.
的取值范围.
(本小题满分14分)
已知函数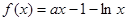
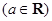 .
.
(1)讨论函数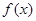 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(2)若函数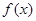 在
在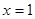 处取得极值,对
处取得极值,对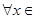
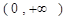 ,
,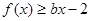 恒成立,
恒成立,
求实数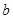 的取值范围;
的取值范围;
(3)当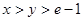 时,求证:
时,求证: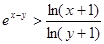 .
.
(本小题满分13分)
已知函数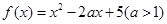 .
.
(1) 若函数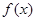 的定义域和值域均为
的定义域和值域均为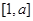 ,求实数
,求实数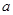 的值;
的值;
(2) 若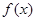 在区间
在区间 上是减函数,且对任意的
上是减函数,且对任意的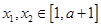 ,
,
总有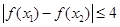 ,求实数
,求实数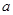 的取值范围;
的取值范围;
(3) 若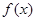 在
在 上有零点,求实数
上有零点,求实数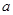 的取值范围.
的取值范围.
(本小题满分12分)
已知某食品厂需要定期购买食品配料,该厂每天需要食品配料200千克,配料的价格为 元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用(若
元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用(若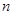 天购买一次,需要支付
天购买一次,需要支付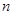 天的保管费)。其标准如下: 7天以内(含7天),无论重量多少,均按10元/天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元/千克支付.
天的保管费)。其标准如下: 7天以内(含7天),无论重量多少,均按10元/天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元/千克支付.
(1)当9天购买一次配料时,求该厂用于配料的保管费用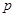 是多少元?[
是多少元?[
(2)设该厂 天购买一次配料,求该厂在这
天购买一次配料,求该厂在这 天中用于配料的总费用
天中用于配料的总费用 (元)关于
(元)关于 的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?
的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?
(本小题满分12分)
已知函数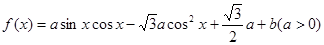
(1)求函数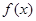 的单调递减区间;
的单调递减区间;
(2)设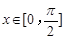 ,
,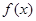 的最小值是
的最小值是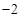 ,最大值是
,最大值是 ,求实数
,求实数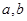 的值.
的值.