观察以下各等式: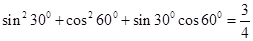
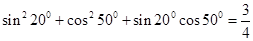
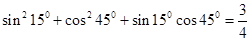 ,
,
分析上述各式的共同特点,猜想出反映一般规律的等式,并对等式的正确性利用综合法作出证明.
已知等差数列 的公差大于0,且
的公差大于0,且 是方程
是方程 的两根,数列
的两根,数列 的前n项的和为
的前n项的和为 ,且
,且 (
( ).
).
(1)求数列 ,
, 的通项公式;
的通项公式;
(2) 记 ,求证:
,求证: .
.
已知某几何体的直观图和三视图如下图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形
(1)求证: ; (2)求证:
; (2)求证:
 ;
;
(3)设 为
为 中点,在
中点,在 边上找一点
边上找一点 ,使
,使
 平面
平面 ,并求
,并求 的值.
的值.

某中学校本课程共开设了A,B,C,D共4门选修课,每个学生必须且只能选修1门选修课,现有该校的甲、乙、丙3名学生:
(1)求这3名学生选修课所有选法的总数;
(2)求恰有2门选修课没有被这3名学生选择的概率;
(3)求A选修课被这3名学生选择的人数的数学期望.
已知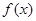 是定义在R上的奇函数,当
是定义在R上的奇函数,当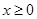 时,
时,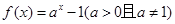 .
.
(1)求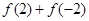 的值;
的值;
(2)求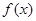 的解析式;
的解析式;
(3)解关于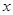 的不等式
的不等式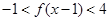 ,结果用集合或区间表示.
,结果用集合或区间表示.
已知坐标平面上点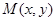 与两个定点
与两个定点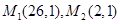 的距离之比等于5.
的距离之比等于5.
(1)求点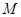 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;
(2)记(1)中的轨迹为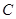 ,过点
,过点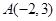 的直线
的直线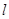 被
被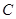 所截得的线段的长为8,求直线
所截得的线段的长为8,求直线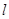 的方程
的方程