已知某几何体的直观图和三视图如下图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形
(1)求证: ; (2)求证:
; (2)求证:
 ;
;
(3)设 为
为 中点,在
中点,在 边上找一点
边上找一点 ,使
,使
 平面
平面 ,并求
,并求 的值.
的值.

(本小题满分15分)
设等差数列 的前
的前 项和为
项和为 且
且 .(1)求数列
.(1)求数列 的通项公式及前
的通项公式及前 项和公式;
项和公式;
(2)设数列 的通项公式为
的通项公式为 (t为正整数),问: 是否存在正整数t,使得
(t为正整数),问: 是否存在正整数t,使得
 成等差数列?若存在,求出t和m的值;若不存在,请说明理由.
成等差数列?若存在,求出t和m的值;若不存在,请说明理由.
(本小题满分15分)
如图所示,一科学考察船从港口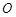 出发,沿北偏东
出发,沿北偏东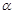 角的射线
角的射线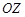 方向航行,而在离港口
方向航行,而在离港口 (
(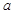 为正常数)海里的北偏东
为正常数)海里的北偏东 角的A处有一个供给科考船物资的小岛,其中
角的A处有一个供给科考船物资的小岛,其中 ,
,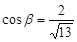 .现指挥部需要紧急征调沿海岸线港口
.现指挥部需要紧急征调沿海岸线港口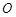 正东m(
正东m( )海里的B处的补给船,速往小岛A装运物资供给科考船,该船沿BA方向全速追赶科考船,并在C处相遇.经测算当两船运行的航向与海岸线OB围成的三角形OBC的面积最小时,这种补给最适宜.
)海里的B处的补给船,速往小岛A装运物资供给科考船,该船沿BA方向全速追赶科考船,并在C处相遇.经测算当两船运行的航向与海岸线OB围成的三角形OBC的面积最小时,这种补给最适宜.
⑴ 求S关于m的函数关系式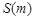 ;
;
⑵ 应征调m为何值处的船只,补给最适宜.
(本小题满分14分)
1.如图,矩形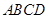 中,
中,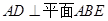 ,
,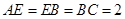 ,
,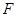 为
为 上的点,且
上的点,且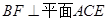 ,
,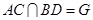 .(Ⅰ)求证:
.(Ⅰ)求证: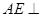 平面
平面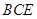 ;(Ⅱ)求证:
;(Ⅱ)求证: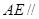 平面
平面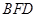 ;(Ⅲ)求三棱锥
;(Ⅲ)求三棱锥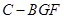 的体积.
的体积.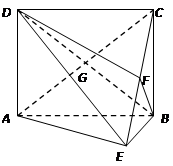
(本小题满分14分)
设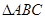 的内角
的内角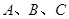 所对的边分别为
所对的边分别为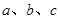 .已知
.已知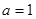 ,
,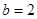 ,
, .
.
(Ⅰ)求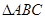 的周长;
的周长;
(Ⅱ)求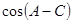 的值.
的值.
已知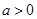 ,函数
,函数 (
( 的图像连续不断)
的图像连续不断)
(Ⅰ)求 的单调区间;
的单调区间;
(Ⅱ)当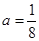 时,证明:存在
时,证明:存在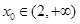 ,使
,使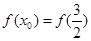 ;
;
(Ⅲ)若存在均属于区间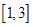 的
的 ,且
,且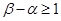 ,使
,使 ,证明
,证明 .
.