(年浙江杭州12分)复习课中,教师给出关于x的函数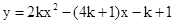 (k是实数).
(k是实数).
教师:请独立思考,并把探索发现的与该函数有关的结论(性质)写到黑板上.
学生思考后,黑板上出现了一些结论. 教师作为活动一员,又补充一些结论,并从中选择如下四条:
①存在函数,其图像经过(1,0)点;
②函数图像与坐标轴总有三个不同的交点;
③当 时,不是y随x的增大而增大就是y随x的增大而减小;
时,不是y随x的增大而增大就是y随x的增大而减小;
④若函数有最大值,则最大值必为正数,若函数有最小值,则最小值必为负数;
教师:请你分别判断四条结论的真假,并给出理由,最后简单写出解决问题时所用的数学方法.
在一个不透明的袋子中有一个黑球 和两个白球 , (除颜色外其他均相同).用树状图(或列表法)解答下列问题:
(1)小丽第一次从袋子中摸出一个球不放回,第二次又从袋子中摸出一个球.则小丽两次都摸到白球的概率是多少?
(2)小强第一次从袋子中摸出一个球,摸到黑球不放回,摸到白球放回;第二次又从袋子中摸出一个球,则小强两次都摸到白球的概率是多少?
已知关于 的一元二次方程: .
(1)求证:对于任意实数 ,方程都有实数根;
(2)当 为何值时,方程的两个根互为相反数?请说明理由.
我们知道,经过原点的抛物线可以用 表示,对于这样的抛物线:
(1)当抛物线经过点 和 时,求抛物线的表达式;
(2)当抛物线的顶点在直线 上时,求 的值;
(3)如图,现有一组这样的抛物线,它们的顶点 、 、 , 在直线 上,横坐标依次为 , , , , 为正整数,且 ,分别过每个顶点作 轴的垂线,垂足记为 、 , , ,以线段 为边向左作正方形 ,如果这组抛物线中的某一条经过点 ,求此时满足条件的正方形 的边长.

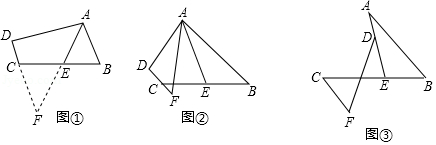
(1)阅读理解:如图①,在四边形 中, , 是 的中点,若 是 的平分线,试判断 , , 之间的等量关系.
解决此问题可以用如下方法:延长 交 的延长线于点 ,易证 ,得到 ,从而把 , , 转化在一个三角形中即可判断.
、 、 之间的等量关系为 ;
(2)问题探究:如图②,在四边形 中, , 与 的延长线交于点 , 是 的中点,若 是 的平分线,试探究 , , 之间的等量关系,并证明你的结论.
(3)问题解决:如图③, , 与 交于点 , ,点 在线段 上,且 ,试判断 、 、 之间的数量关系,并证明你的结论.
如图,直线 与反比例函数 的图象交于点 ,与 轴交于点 ,平行于 轴的直线 交反比例函数的图象于点 ,交 于点 ,连接 .
(1)求 的值和反比例函数的表达式;
(2)直线 沿 轴方向平移,当 为何值时, 的面积最大?
