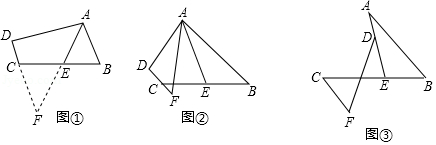
（1）阅读理解：如图①，在四边形 中， ， 是 的中点，若 是 的平分线，试判断 ， ， 之间的等量关系．
解决此问题可以用如下方法：延长 交 的延长线于点 ，易证 ，得到 ，从而把 ， ， 转化在一个三角形中即可判断．
、 、 之间的等量关系为 ；
（2）问题探究：如图②，在四边形 中， ， 与 的延长线交于点 ， 是 的中点，若 是 的平分线，试探究 ， ， 之间的等量关系，并证明你的结论．
（3）问题解决：如图③， ， 与 交于点 ， ，点 在线段 上，且 ，试判断 、 、 之间的数量关系，并证明你的结论．
如图，矩形ABCD中，AB=4cm，AD="3" cm，点P从A点出发，以5cm/s的速度，沿AC向C作匀速运动；与此同时，点Q也从A点出发，以4cm/s的速度，沿射线AB作匀速运动。当P运动到C点时，P、Q都停止运动。设点P运动的时间为ts。
（1）当P异于A．C时，证明：以P为圆心、PQ长为半径的圆总是与边AB相切；
（2）在整个运动过程中，t为怎样的值时，以P为圆心、PQ长为半径的圆与边BC分别有1个公共点和2个公共点？
如图，等腰梯形MNPQ的上底长为2，腰长为3，一个底角为60°．正方形ABCD的边长为1，它的一边AD在MN上，且顶点A与M重合．现将正方形ABCD在梯形的外面沿边MN、NP、PQ进行翻滚，翻滚到有一个顶点与Q重合即停止滚动．
求正方形在整个翻滚过程中点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S．
如图，在平面坐标系中，直线y=﹣x+2与x轴，y轴分别交于点A，点B，动点P（a，b）在第一象限内，由点P向x轴，y轴所作的垂线PM，PN（垂足为M，N）分别与直线AB相交于点E，点F，当点P（a，b）运动时，矩形PMON的面积为定值2．当点E，F都在线段AB上时，由三条线段AE，EF，BF组成一个三角形，记此三角形的外接圆面积为S1，△OEF的面积为S2．试探究：
是否存在最大值？若存在，请求出该最大值；若不存在，请说明理由．
如图1，矩形MNPQ中，点E、F、G、H分别在NP、PQ、QM、MN上，若
，则称四边形EFGH为矩形MNPQ的反射四边形．在图2、图3中，四边形ABCD为矩形，且
，
．
（1）在图2、图3中，点E、F分别在BC、CD边上，图2中的四边形EFGH是利用正方形网格在图上画出的矩形ABCD的反射四边形．请你利用正方形网格在图3上画出矩形ABCD的反射四边形EFGH；
（2）图2、图3中矩形ABCD的反射四边形EFGH的周长是否为定值？若是定值，请直接写出这个定值；若不是定值，请直接写出图2、图3中矩形ABCD的反射四边形EFGH的周长各是多少；
（3）图2、图3中矩形ABCD的反射四边形EFGH的面积是否为定值？若是定值，请直接写出这个定值；若不是定值，请直接写出图2、图3中矩形ABCD的反射四边形EFGH的面积各是多少．
如图，直线l1与x轴、y轴分别交于A、B两点，直线l2与直线l1关于x轴对称，已知直线l1的解析式为
．
（1）求直线l2的解析式；
（2）过A点在△ABC的外部作一条直线l3，过点B作BE⊥l3于E，过点C作CF⊥l3于F，请画出图形并求证：BE+CF=EF；
（3）△ABC沿y轴向下平移，AB边交x轴于点P，过P点的直线与AC边的延长线相交于点Q，与y轴相交于点M，且BP=CQ，在△ABC平移的过程中，①OM为定值；②MC为定值．在这两个结论中，有且只有一个是正确的，请找出正确的结论，并求出其值．