(年甘肃白银、定西、平凉、酒泉、临夏12分)如图,在平面直角坐标系xOy中,顶点为M的抛物线是由抛物线y=x2﹣3向右平移一个单位后得到的,它与y轴负半轴交于点A,点B在该抛物线上,且横坐标为3.
(1)求点M、A、B坐标;
(2)连结AB、AM、BM,求∠ABM的正切值;
(3)点P是顶点为M的抛物线上一点,且位于对称轴的右侧,设PO与x正半轴的夹角为α,当α=∠ABM时,求P点坐标.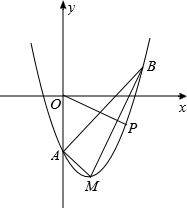
为了解某市九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分
段(A:50分;B:49-45分;C:44-40分;D:39-30分;E:29-0分)统计如下: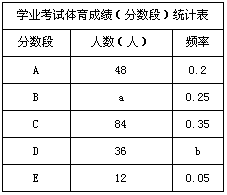
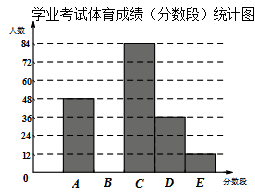
根据上面提供的信息,回答下列问题:
(1)在统计表中,a的值为 ▲ ,b的值为 ▲ ,并将统计图补充完整(温馨提示:作图时别忘了用0.5毫米及以上的黑色签字笔涂黑);
(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数. ”请问:甲同学的体育成绩应在什么分数段内?▲(填相应分数段的字母)
(3)如果把成绩在40分以上(含40分)定为优秀,那么该市今年10440名九年级学生中体育成绩为优秀的学生人数约有多少名?
商场某种商品平均每天可销售30件,每件盈利50元. 为了尽快减少库存,商场决定采取适当的降价措施. 经调查发现,每件商品每降价1元,商场平均每天可多售出 2件.设每件商品降价x元. 据此规律,请回答:
(1)商场日销售量增加件,每件商品盈利元(用含x的代数式表示);
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
如图,已知E、F是□ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.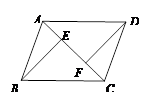
(1)求证:△ABE≌△CDF;
(2)请写出图中除△ABE≌△CDF外其余两对全等三角形(不再添加辅助线).
(1)计算: 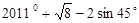 ;
;
(2)解分式方程: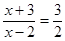 .
.
如图,在平面直角坐标系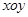 中,把抛物线
中,把抛物线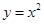 向左平移1个单位,再向下平移4个单位,得到抛物线
向左平移1个单位,再向下平移4个单位,得到抛物线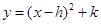 .所得抛物线与
.所得抛物线与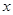 轴交于
轴交于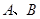 两点(点
两点(点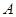 在点
在点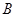 的左边),与
的左边),与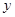 轴交于点
轴交于点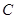 ,顶点为
,顶点为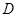 .
.
(1)写出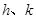 的值;
的值;
(2)判断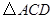 的形状,并说明理由;
的形状,并说明理由;
(3)在线段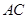 上是否存在点
上是否存在点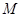 ,使
,使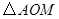 ∽
∽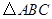 ?若存在,求出点
?若存在,求出点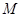 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.