(年湖北鄂州10分)大学生小张利用暑假50天在一超市勤工俭学,被安排销售一款成本为40元/件的新型商品,此类新型商品在第x天的销售量p件与销售的天数x的关系如下表:
| x(天) |
1 |
2 |
3 |
… |
50 |
| p(件) |
118 |
116 |
114 |
… |
20 |
销售单价q(元/件)与x满足:当1≤x<25时q=x+60;当25≤x≤50时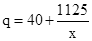 .
.
(1)请分析表格中销售量p与x的关系,求出销售量p与x的函数关系.
(2)求该超市销售该新商品第x天获得的利润y元关于x的函数关系式.
(3)这50天中,该超市第几天获得利润最大?最大利润为多少?
如图,四边形OBCD中的三个顶点在⊙O上,点A是⊙O上的一个动点(不与点B、C、D重合).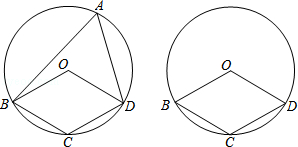
(1)若点A在优弧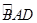 上,且圆心O在∠BAD的内部,已知∠BOD=120°,则∠OBA+∠ODA= .
上,且圆心O在∠BAD的内部,已知∠BOD=120°,则∠OBA+∠ODA= .
(2)若四边形OBCD为平行四边形.
①当圆心O在∠BAD的内部时,求∠OBA+∠ODA的度数;
②当圆心O在∠BAD的外部时,请画出图形并直接写出∠OBA与∠ODA的数量关系.
目前,各大城市都在积极推进公共自行车建设,努力为人们绿色出行带来方便.图(1)所示的是一辆自行车的实物图.图(2)是自行车的车架示意图.CE=30cm,DE=20cm,AD=25cm,DE⊥AC于点E,座杆CF的长为15cm,点A、E、C、F在同一直线上,且∠CAB=75°.
(1)求车架中AE的长;
(2)求车座点F到车架AB的距离.(结果精确到1cm.参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
如图,一次函数y=kx+b的图象经过点A(6,0),点B(2,2),且与y轴相交于点C.请根据以上信息(不再添加其他条件),提出一个问题并尝试解答.你提出的问题是 ;并请写出你的解答过程.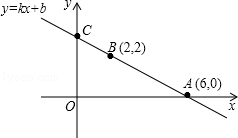
(1)计算: ﹣(π﹣3.14)0+2﹣1;
﹣(π﹣3.14)0+2﹣1;
(2)化简:(a+3)2﹣a(a+3).
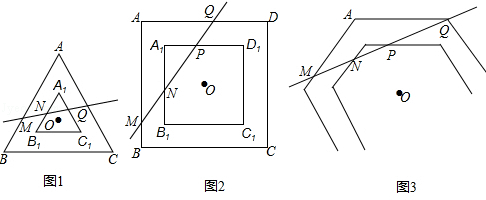
(1)如图1,两个等边三角形ABC和A1B1C1的中心(点O)相同,且满足AB∥A1B1,BC∥B1C1,AC∥A1C1,可知AB与 A1B1,BC与B1C1,AC与A1C1之间的距离相等,直线MQ分别交三角形相邻两边于点M、N、P、Q,与AB所成夹角为∠α,
①当∠α=30°时,求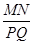 的值;
的值;
②当30°<∠α<90°,请用含∠α的式子表示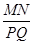 ;
;
(2)如图2,两个正方形ABCD和A1B1C1D1的中心(点O)相同,且满足AB∥A1B1,BC∥B1C1,CD∥C1D1,AD∥A1D1,可知AB与A1B1,BC与B1C1,CD与C1D1,AD与A1D1之间的距离相等,直线MQ分别交正方形相邻两边于点M、N、P、Q,与AB所成夹角为∠α,
①当∠α=30°时,求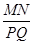 的值;
的值;
②当0°<∠α<90°,请用含∠α的式子表示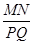 ;
;
(3)根据(1)、(2)的研究,如果正n边形(n>4)的位置关系也满足同样的条件(如图3),正n边形相邻两边被直线MQ截得的两条线段为MN,PQ,请用含m,∠α(0°<∠α<90°)的式子表示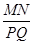 .
.