如图,四边形OBCD中的三个顶点在⊙O上,点A是⊙O上的一个动点(不与点B、C、D重合).
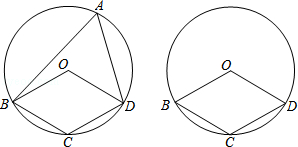
(1)若点A在优弧 上,且圆心O在∠BAD的内部,已知∠BOD=120°,则∠OBA+∠ODA= .
上,且圆心O在∠BAD的内部,已知∠BOD=120°,则∠OBA+∠ODA= .
(2)若四边形OBCD为平行四边形.
①当圆心O在∠BAD的内部时,求∠OBA+∠ODA的度数;
②当圆心O在∠BAD的外部时,请画出图形并直接写出∠OBA与∠ODA的数量关系.
如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(1,0),C(0,﹣3).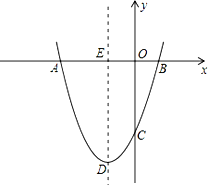
(1)求抛物线的解析式;
(2)若点P为第三象限内抛物线上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
如图,二次函数的图象与x轴交与A(4,0),并且OA=OC=4OB,点P为过A、B、C三点的抛物线上一动点.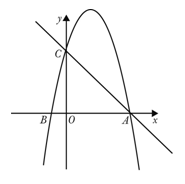
(1)求点B、点C的坐标并求此抛物线的解析式;
(2)是否存在点P,使得△ACP是以点C为直角顶点的直角三角形?若存在,求出点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
在平面直角坐标系中,抛物线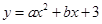 与x轴的两个交点分别为A(-3,0),B(1,0),过顶点C作CH⊥x轴于点H.
与x轴的两个交点分别为A(-3,0),B(1,0),过顶点C作CH⊥x轴于点H.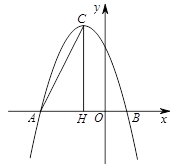
(1)a= ,b= ,顶点C的坐标为 .
(2)在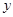 轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由.
轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由.
(3)若点P为x轴上方的抛物线上一动点(点P与顶点C不重合),PQ⊥AC于点Q,当△PCQ与△ACH相似时,求点P的坐标.
请以下列三个代数式中任选两个构造一个分式,并化简该分式.
a2﹣1;ab﹣b;b+ab.
给定下面一列分式: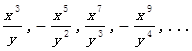 ,(其中x≠0)
,(其中x≠0)
(1)把任意一个分式除以前面一个分式,你发现了什么规律?
(2)根据你发现的规律,试写出给定的那列分式中的第7个分式.