（年宁夏区10分）某花店计划下个月每天购进80只玫瑰花进行销-优题课

（年宁夏区10分）某花店计划下个月每天购进80只玫瑰花进行销售，若下个月按30天计算，每售出1只玫瑰花获利润5元，未售出的玫瑰花每只亏损3元．以x（0＜x≤80）表示下个月内每天售出的只数，y（单位：元）表示下个月每天销售玫瑰花的利润．根据历史资料，得到同期下个月内市场销售量的频率分布直方图（每个组距包含左边的数，但不包含右边的数）如下图：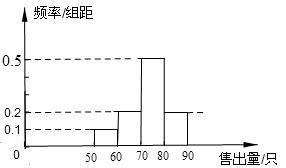

（1）求y关于x的函数关系式；
（2）根据频率分布直方图，计算下个月内销售利润少于320元的天数；
（3）根据历史资料，在70≤x＜80这个组内的销售情况如下表：

销售量/只	70	72	74	75	77	79
天数	1	2	3	4	3	2

计算该组内平均每天销售玫瑰花的只数．

科目数学题型解答题难度中等

如图，已知一次函数 $y_{1} = k_{1} x + b (k_{1} \neq 0)$ 与反比例函数 $y_{2} = \frac{k_{2}}{x} (k_{2} \neq 0)$ 的图象交于 $A (4, 1)$ ， $B (n, - 2)$ 两点．

（1）求一次函数与反比例函数的解析式；

（2）请根据图象直接写出 $y_{1} < y_{2}$ 时 $x$ 的取值范围．

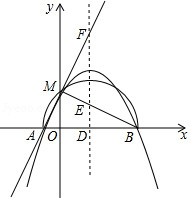
已知二次函数 $y = - x^{2} + bx + c + 1$ ，

①当 $b = 1$ 时，求这个二次函数的对称轴的方程；

②若 $c = - \frac{1}{4} b^{2} - 2 b$ ，问： $b$ 为何值时，二次函数的图象与 $x$ 轴相切？

③若二次函数的图象与 $x$ 轴交于点 $A (x_{1}$ ， $0)$ ， $B (x_{2}$ ， $0)$ ，且 $x_{1} < x_{2}$ ， $b > 0$ ，与 $y$ 轴的正半轴交于点 $M$ ，以 $AB$ 为直径的半圆恰好过点 $M$ ，二次函数的对称轴 $l$ 与 $x$ 轴、直线 $BM$ 、直线 $AM$ 分别交于点 $D$ 、 $E$ 、 $F$ ，且满足 $\frac{DE}{EF} = \frac{1}{3}$ ，求二次函数的表达式．

如图所示， $Rt Δ PAB$ 的直角顶点 $P (3, 4)$ 在函数 $y = \frac{k}{x} (x > 0)$ 的图象上，顶点 $A$ 、 $B$ 在函数 $y = \frac{t}{x} (x > 0, 0 < t < k)$ 的图象上， $PA / / y$ 轴，连接 $OP$ ， $OA$ ，记 $ΔOPA$ 的面积为 $S_{ΔOPA}$ ， $ΔPAB$ 的面积为 $S_{ΔPAB}$ ，设 $w = S_{ΔOPA} - S_{ΔPAB}$ ．

①求 $k$ 的值以及 $w$ 关于 $t$ 的表达式；

②若用 $w_{\max}$ 和 $w_{\min}$ 分别表示函数 $w$ 的最大值和最小值，令 $T = w_{\max} + a^{2} - a$ ，其中 $a$ 为实数，求 $T_{\min}$ ．

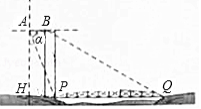
如图示一架水平飞行的无人机 $AB$ 的尾端点 $A$ 测得正前方的桥的左端点 $P$ 的

俯角为 $α$ 其中 $\tan α = 2 \sqrt{3}$ ，无人机的飞行高度 $AH$ 为 $500 \sqrt{3}$ 米，桥的长度为1255米．

①求点 $H$ 到桥左端点 $P$ 的距离；

②若无人机前端点 $B$ 测得正前方的桥的右端点 $Q$ 的俯角为 $30 °$ ，求这架无人机的长度 $AB$ ．

如图示，正方形 $ABCD$ 的顶点 $A$ 在等腰直角三角形 $DEF$ 的斜边 $EF$ 上， $EF$ 与 $BC$ 相交于点 $G$ ，连接 $CF$ ．

①求证： $ΔDAE ≅ ΔDCF$ ；

②求证： $ΔABG ∽ ΔCFG$ ．

试卷网试题网古诗词网作文网范文网