（2014年广西桂林12分）如图，已知抛物线yax2bx4与-优题课

（20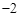14年广西桂林12分）如图，已知抛物线y=ax²+bx+4与x轴交于A（,0）、B两点，与y轴交于C点，其对称轴为直线x=1.
（1）直接写出抛物线的解析式：
（2）把线段AC沿x轴向右平移，设平移后A、C的对应点分别为A′、C′，当C′落在抛物线上时，求A′、C′的坐标；
（3）除（2）中的点A′、C′外，在x轴和抛物线上是否还分别存在点E、F，使得以A、C、E、F为顶点的四边形为平行四边形，若存在，求出E、F的坐标；若不存在，请说明理由.

科目数学题型解答题难度中等

为迎接建党一百周年，我市计划用两种花卉对某广场进行美化．已知用600元购买 $A$ 种花卉与用900元购买 $B$ 种花卉的数量相等，且 $B$ 种花卉每盆比 $A$ 种花卉多0.5元．

（1） $A$ ， $B$ 两种花卉每盆各多少元？

（2）计划购买 $A$ ， $B$ 两种花卉共6000盆，其中 $A$ 种花卉的数量不超过 $B$ 种花卉数量的 $\frac{1}{3}$ ，求购买 $A$ 种花卉多少盆时，购买这批花卉总费用最低，最低费用是多少元？

为扎实推进“五育并举”工作，某校根据课外活动时间，开设了书法、健美操、乒乓球和朗诵四个社团活动，每个学生选择一项活动参加，为了了解活动开展情况，学校随机抽取了部分学生进行调查，将调查结果绘制成条形统计图和扇形统计图：

请根据以上的信息，回答下列问题：

（1）抽取的学生有　　人， $n =$ 　　， $a =$ 　　；

（2）补全条形统计图；

（3）若该校有学生3200人，估计参加书法社团活动的学生人数．

先化简，再求值： $\frac{2 a + 1}{a + 1} + \frac{a^{2} - 2 a}{a^{2} - 1} \div (\frac{2 a - 1}{a - 1} - a - 1)$ ，其中 $a = - \frac{3}{2}$ ．

如图，直线 $y = - \frac{1}{2} x + \frac{3}{2}$ 分别交 $x$ 轴、 $y$ 轴于点 $A$ ， $B$ ，过点 $A$ 的抛物线 $y = - x^{2} + bx + c$ 与 $x$ 轴的另一交点为 $C$ ，与 $y$ 轴交于点 $D (0, 3)$ ，抛物线的对称轴 $l$ 交 $AD$ 于点 $E$ ，连接 $OE$ 交 $AB$ 于点 $F$ ．

（1）求抛物线的解析式；

（2）求证： $OE ⊥ AB$ ；

（3） $P$ 为抛物线上的一动点，直线 $PO$ 交 $AD$ 于点 $M$ ，是否存在这样的点 $P$ ，使以 $A$ ， $O$ ， $M$ 为顶点的三角形与 $ΔACD$ 相似？若存在，求点 $P$ 的横坐标；若不存在，请说明理由．

研究立体图形问题的基本思路是把立体图形问题转化为平面图形问题．

（1）阅读材料

立体图形中既不相交也不平行的两条直线所成的角，就是将直线平移使其相交所成的角．

例如，正方体 $ABCD - A' B' C' D'$ （图 $1)$ ，因为在平面 $AA' C' C$ 中， $CC' / / A A^{'}$ ， $AA'$ 与 $AB$ 相交于点 $A$ ，所以直线 $AB$ 与 $AA'$ 所成的 $∠ BAA'$ 就是既不相交也不平行的两条直线 $AB$ 与 $CC'$ 所成的角．

解决问题

如图1，已知正方体 $ABCD - A' B' C' D^{'}$ ，求既不相交也不平行的两直线 $BA'$ 与 $AC$ 所成角的大小．

（2）如图2， $M$ ， $N$ 是正方体相邻两个面上的点；

①下列甲、乙、丙三个图形中，只有一个图形可以作为图2的展开图，这个图形是　　；

②在所选正确展开图中，若点 $M$ 到 $AB$ ， $BC$ 的距离分别是2和5，点 $N$ 到 $BD$ ， $BC$ 的距离分别是4和3， $P$ 是 $AB$ 上一动点，求 $PM + PN$ 的最小值．