研究立体图形问题的基本思路是把立体图形问题转化为平面图形问题.
(1)阅读材料
立体图形中既不相交也不平行的两条直线所成的角,就是将直线平移使其相交所成的角.
例如,正方体 (图 ,因为在平面 中, , 与 相交于点 ,所以直线 与 所成的 就是既不相交也不平行的两条直线 与 所成的角.
解决问题
如图1,已知正方体 ,求既不相交也不平行的两直线 与 所成角的大小.

(2)如图2, , 是正方体相邻两个面上的点;
①下列甲、乙、丙三个图形中,只有一个图形可以作为图2的展开图,这个图形是 ;
②在所选正确展开图中,若点 到 , 的距离分别是2和5,点 到 , 的距离分别是4和3, 是 上一动点,求 的最小值.

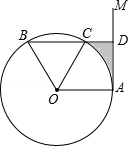
如图,点 A是直线 AM与⊙ O的交点,点 B在⊙ O上, BD⊥ AM垂足为 D, BD与⊙ O交于点 C, OC平分∠ AOB,∠ B=60°.
(1)求证: AM是⊙ O的切线;
(2)若 DC=2,求图中阴影部分的面积(结果保留π和根号).
为了尽快实施"脱贫致富奔小康"宏伟意图,某县扶贫工作队为朝阳沟村购买了一批苹果树苗和梨树苗,已知一棵苹果树苗比一棵梨树苗贵2元,购买苹果树苗的费用和购买梨树苗的费用分别是3500元和2500元.
(1)若两种树苗购买的棵数一样多,求梨树苗的单价;
(2)若两种树苗共购买1100棵,且购买两种树苗的总费用不超过6000元,根据(1)中两种树苗的单价,求梨树苗至少购买多少棵.
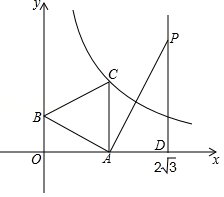
如图,一次函数 y=﹣ x+1的图象与 x轴、 y轴分别交于点 A、 B,以线段 AB为边在第一象限作等边△ ABC.
(1)若点 C在反比例函数 y= 的图象上,求该反比例函数的解析式;
(2)点 P(2 , m)在第一象限,过点 P作 x轴的垂线,垂足为 D,当△ PAD与△ OAB相似时, P点是否在(1)中反比例函数图象上?如果在,求出 P点坐标;如果不在,请加以说明.
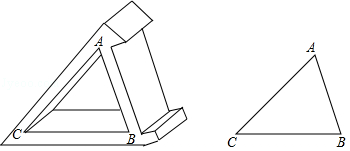
王浩同学用木板制作一个带有卡槽的三角形手机架,如图所示.已知 AC=20 cm, BC=18 cm,∠ ACB=50°,王浩的手机长度为17 cm,宽为8 cm,王浩同学能否将手机放入卡槽 AB内?请说明你的理由.(提示:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2)
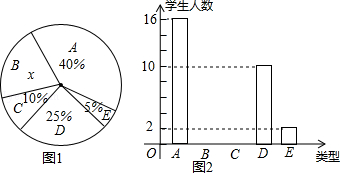
为了增强中学生的体质,某校食堂每天都为学生提供一定数量的水果,学校李老师为了了解学生喜欢吃哪种水果,进行了抽样调查,调查分为五种类型: A.喜欢吃苹果的学生; B.喜欢吃桔子的学生; C.喜欢吃梨的学生; D.喜欢吃香蕉的学生; E.喜欢吃西瓜的学生,并将调查结果绘制成图1和图2的统计图(不完整).请根据图中提供的数据解答下列问题:
(1)求此次抽查的学生人数;
(2)将图2补充完整,并求图1中的 x;
(3)现有5名学生,其中 A类型3名, B类型2名,从中任选2名学生参加体能测试,求这两名学生为同一类型的概率(用列表法或树状图法)