（年湖北鄂州12分）如图，在平面直角坐标系xOy中，一次函数
的图象与x轴交于A（﹣1，0），与y轴交于点C．以直线x=2为对称轴的抛物线C1：y=ax2+bx+c（a≠0）经过A、C两点，并与x轴正半轴交于点B．
（1）求m的值及抛物线C1：y=ax2+bx+c（a≠0）的函数表达式．
（2）设点D（0，
），若F是抛物线C1：y=ax2+bx+c（a≠0）对称轴上使得△ADF的周长取得最小值的点，过F任意作一条与y轴不平行的直线交抛物线C1于M1（x1，y1），M2（x2，y2）两点，试探究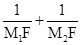
是否为定值？请说明理由．
（3）将抛物线C1作适当平移，得到抛物线C2：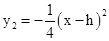
，h＞1．若当1＜x≤m时，y2≥﹣x恒成立，求m的最大值．
某校要从甲、乙两名跳高运动员中挑选一人参加一项校际比赛，在最近的8次选拔赛中，他们的成绩（单位：m）如下：
甲：1.70，1.65，1.68，1.69，1.72，1.73，1.68，1.67
乙：1.60，1.73，1.72，1.61，1.62，1.71，1.70，1.75
（1）他们的平均成绩分别是多少？
（2）哪个人的成绩更为稳定？
（3）经预测，跳高1.65m就很可能获得冠军，该校为了获取跳高比赛冠军，可能选哪位运动员参赛？若预测跳高1.70m方可获得冠军呢？
为了考察甲、乙两种农作物的长势，分别从中抽取了10株苗，测得苗高如下：（单位：mm）
甲：9，10，11，12，7，13，10，8，12，8
乙：8，13，12，11，10，12，7，7，9，11
请你经过计算后回答如下问题：
（1）哪种农作物的10株苗长的比较高？
（2）哪种农作物的10株苗长的比较整齐？
问题：那边草地上有六个人正在玩游戏，他们年龄的平均数是15岁. 请想象一下是怎样年龄的六个人在玩游戏？
小飞认为：那一定是一群中学生在玩游戏.
你认为小飞的想法肯定正确吗？如果你认为不正确，那么指出错误的原因.
某公司有10名销售业务员，去年每人完成的销售额情况如下表：
| 销售额（万元） |
3 |
4 |
5 |
6 |
7 |
8 |
10 |
| 销售人数 |
1 |
3 |
2 |
1 |
1 |
1 |
1 |
问题：（1）求10名销售员销售额的平均数、中位数和众数（单位：万元）；
（2）为了调动员工积极性，公司准备采取超额有奖措施，请问把标准定为多少万元时最合适？
某鞋店销售了9双鞋，各种尺码的销售量如下：
| 鞋的尺码 |
20 |
21 |
22 |
23 |
| 销售量（双） |
1 |
2 |
4 |
2 |
（1）计算这9双鞋尺码的平均数、中位数和众数.
（2）哪一个指标是鞋厂最感兴趣的指标？哪一个指标是鞋厂最不感兴趣的？