（2014年湖北宜昌12分）如图，在平面直角坐标系中，已知点P（0，4），点A在线段OP上，点B在x轴正半轴上，且AP=OB=t， 0＜t＜4，以AB为边在第一象限内作正方形ABCD；过点C、D依次向x轴、y轴作垂线，垂足为M，N，设过O，C两点的抛物线为y=ax2+bx+c．
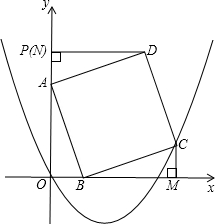
（1）填空：△AOB≌△ ≌△BMC（不需证明）；用含t的代数式表示A点纵坐标：A（0， ；
（2）求点C的坐标，并用含a，t的代数式表示b；
（3）当t=1时，连接OD，若此时抛物线与线段OD只有唯一的公共点O，求a的取值范围；
（4）当抛物线开口向上，对称轴是直线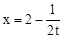
，顶点随着t的增大向上移动时，求t的取值范围．
已知四边形ABCD中，E、F分别是AB、AD边上的点，DE与CF交于点G．
（1）如图①，若四边形ABCD是矩形，且DE⊥CF，求证
；
（2）如图②，若四边形ABCD是平行四边形，试探究：当∠B与∠EGC满足什么关系时，使得成立？并证明你的结论；
（3）如图③，若BA=BC=2，DA=DC=
，∠BAD＝90°，DE⊥CF，试求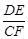
的值．
如图，抛物线y=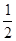
x2+bx－2与x轴交于A、B两点，与y轴交于C点，且A（一1，0）．
（1）求抛物线的解析式及顶点D的坐标；
（2）判断△ABC的形状，证明你的结论；
（3）点M是抛物线对称轴上的一个动点，当△ACM周长最小时，求点M的坐标及△ACM的最小周长．
某学校将周三“阳光体育”项目定为跳绳活动，为此学校准备购置长、短两种跳绳若干．已知长跳绳的单价比短跳绳单价的两倍多4元，且购买2条长跳绳与购买5条短跳绳的费用相同．
（1）两种跳绳的单价各是多少元？
（2）若学校准备用不超过2000元的现金购买200条长、短跳绳，且短跳绳的条数不超过长跳绳的6倍，问学校有几种购买方案可供选择？请说明哪种购买方案最省钱？
如图，已知⊙O的直径AB与弦CD相交于点E，AB⊥CD，⊙O的切线BF与弦AD的延长线相交于点F．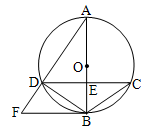
（1）求证：CD∥BF；
（2）若⊙O的半径为5，cos∠BCD=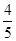
，求线段AD与BF的长．
如图，在马航失联客机“MH370”搜寻中需要确定疑似海面上油污带AB的长度．已知在离地面1500m高度C处的飞机上，测量人员测得正前方A、B两点处的俯角分别为60°和45°．求油污带AB的长．（参考数据：
=1．73）