①计算：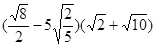
②解方程： 
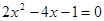
如图，半径为2的⊙C与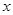
轴的正半轴交于点A，与
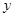轴的正半轴交于点B，点C的坐标为（1，0），若抛物线
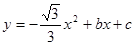过A、B两点。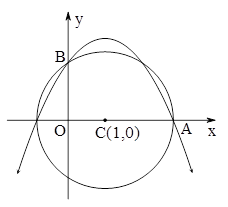
（1）求抛物线的解析式；
（2）在抛物线上是否存在P，使得∠PBO=∠POB？若存在，求出点P的坐标；若不存在说明理由；
（3）若点M是抛物线（在第一象限内的部分）上一点，△MAB的面积为S，求S的最大（小）值。
如图，AB是⊙O的直径，弦DE垂直平分半径OA，C为垂足，DE=3，连结DB，过点E作EM∥BD，交BA的延长线于点M。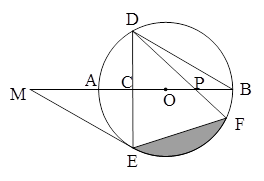
（1）求⊙O的半径；
（2）求证：EM是⊙O的切线；
（3）若弦DF与直径AB相交于点P，当∠DPA=45°时，求图中阴影部分的面积。
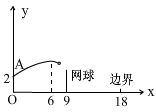
如图，排球运动员站在点O处练习发球，将球从O点正上方2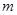
的点A处发出，把球看成点，其运行的高度
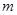（）与运行的水平距离
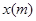满足关系式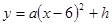
，已知球网与O点的水平距离为9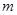，高度为2.43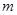，球场的边界距O点水平距离为18。
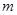（1）当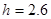
时，求与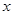
的关系式（不要求写出自变量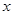的取值范围）；
（2）当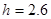时，球能否越过球网？球会不会出界，请说明理由；
（3）若球一定能越过球网，又不出边界，求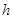
的取值范围。
如图，AB是⊙O的直径，C是⊙O上一点，AD垂直于过C点的切线，垂足为D。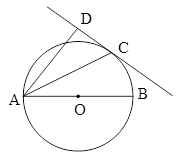
（1）求证：AC平分∠BAD；（2）若AC=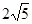
，CD=2，求⊙O的直径。
．