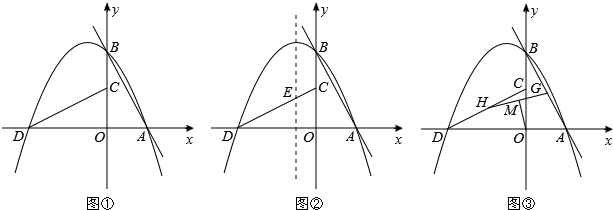
(2014年吉林省10分)如图①,直线l:y=mx+n(m>0,n<0)与x,y轴分别相交于A,B两点,将△AOB绕点O逆时针旋转90°,得到△COD,过点A,B,D的抛物线P叫做l的关联抛物线,而l叫做P的关联直线.
(1)若l:y=﹣2x+2,则P表示的函数解析式为 ;若P:y=﹣x2﹣3x+4,则l表示的函数解析式为 .
(2)求P的对称轴(用含m,n的代数式表示);
(3)如图②,若l:y=﹣2x+4,P的对称轴与CD相交于点E,点F在l上,点Q在P的对称轴上.当以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形时,求点Q的坐标;
(4)如图③,若l:y=mx﹣4m,G为AB中点,H为CD中点,连接GH,M为GH中点,连接OM.若OM=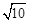 ,直接写出l,P表示的函数解析式.
,直接写出l,P表示的函数解析式.
已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.
在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共5只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
| 摸球的次数n |
100 |
150 |
200 |
500 |
800 |
1000 |
| 摸到白球的次数m |
58 |
96 |
116 |
295 |
484 |
601 |
摸到白球的频率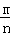 |
0.58 |
0.64 |
0.58 |
0.59 |
0.605 |
0.601 |
(1)请估计:当n很大时,摸到白球的频率将会接近 ;(精确到0.1)
(2)试估算口袋中白种颜色的球有多少只?
(3)请画树状图或列表计算:从中先摸出一球,不放回,再摸出一球;这两只球颜色不同的概率是多少?
如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(4,0),B(0,3).点C的坐标为(0,m),过点C作CE⊥AB于点E,点D为x轴正半轴的一动点,且满足OD=2OC,连结DE,以DE,DA为边作▱DEFA.
(1)当m=1时,求AE的长.
(2)当0<m<3时,若▱DEFA为矩形,求m的值;
(3)是否存在m的值,使得▱DEFA为菱形?若存在,直接写出m的值;若不存在,请说明理由.
如图,边长为4的等边△AOB的顶点O在坐标原点,点A在x轴正半轴上,点B在第一象限.一动点P沿x轴以每秒1个单位长度的速度由点O向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.在点P的运动过程中,线段BP的中点为点E,将线段PE绕点P按顺时针方向旋转60°得PC.
(1)当点P运动到线段OA的中点时,点C的坐标为 ;
(2)在点P从点O到点A的运动过程中,用含t的代数式表示点C的坐标;
(3)在点P从点O到点A的运动过程中,求出点C所经过的路径长.
2013年1月,由于雾霾天气持续笼罩我国中东部大部分地区,口罩市场出现热卖,某旗舰网店用8000元购进甲、乙两种口罩,销售完后共获利2800元,进价和售价如下表:
| 品名 价格 |
甲种口罩 |
乙种口罩 |
| 进价(元/袋) |
20 |
25 |
| 售价(元/袋) |
26 |
35 |
(1)求该网店购进甲、乙两种口罩各多少袋?
(2)该网店第二次以原价购进甲、乙、两种口罩,购进乙种口罩袋数不变,而购进甲种口罩袋数是第一次的2倍.甲种口罩按原售价出售,而乙种口罩让利销售.若两种口罩销售完毕,要使第二次销售活动获利不少于3680元,乙种口罩最低售价为每袋多少元?