（年重庆市B12分）如图1，在□ABCD中，AH⊥DC，垂足为H，AB＝
，AD＝7，AH＝
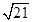.现有两个动点E、F同时从点A出发，分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动. 在点E、F运动过程中，以EF为边作等边△EFG，使△EFG与△ABC在射线AC的同侧，当点E运动到点C时，E、F两点同时停止运动. 设运转时间为t秒.
（1）求线段AC的长；
（2）在整个运动过程中，设等边△EFG与△ABC重叠部分的面积为S，请直接写出S与t之间的函数关系式，并写出相应的自变量t的取值范围；
（3）当等边△EFG的顶点E到达点C时，如图2，将△EFG绕着点C旋转一个角度
. 在旋转过程中，点E与点C重合，F的对应点为F′，G的对应点为G′. 设直线F′G′与射线DC、射线AC分别相交于M、N两点.试问：是否存在点M、N，使得△CMN是以∠MCN为底角的等腰三角形？若存在，请求出线段CM的长度；若不存在，请说明理由.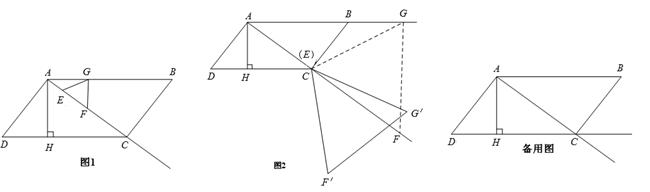
解二元一次方程组
（1）有位同学是这么做的，①+②得4x=20，解得x=5，代入①得y=-3．
∴这个方程组的解为
．该同学解这个二元一次方程组的过程中使用了____________消元法，目的是把二元一次方程组转化为_______________求解；
（2）请你换一种方法来求解该二元一次方程组．
2011年5月9日至14日，德州市共有35000余名学生参加中考体育测试，为了了解九年级男生立定跳远的成绩，从某校随机抽取了50名男生的测试成绩，根据测试评分标准，将他们的得分按优秀、良好、及格、不及格（分别用A、B、C、D表示）四个等级进行统计，并绘制成下面的扇形图和统计表：
| 等级 |
成绩 |
频数（人数） |
频率 |
| A |
90～100 |
19 |
0.38 |
| B |
75～89 |
m |
x |
| C |
60～74 |
n |
y |
| D |
60以下 |
3 |
0.06 |
| 合计 |
50 |
1.00 |
请你根据以上图表提供的信息，解答下列问题：
（1）m=，n=，x=，y=
（2）在扇形图中，C等级所对应的圆心角是；
（3）如果该校九年级共有500名男生参加了立定跳远测试，那么请你估计这些男生成绩等级达到优秀和良好的共有多少人？
今年5月31日是世界卫生组织发起的第25个“世界无烟日”.为了更好地宣传吸烟的危害，某中学八年级一班数学兴趣小组设计了如下调查问卷，在达城中心广场随机调查了部分吸烟人群，并将调查结果绘制成统计图.
根据以上信息，解答下列问题：
（1）本次接受调查的总人数是人，并把条形统计图补充完整.
（2）在扇形统计图中，C选项的人数百分比是，E选项所在扇形的圆心角的度数是.
（3）若通川区约有烟民14万人，试估计对吸烟有害持“无所谓”态度的约有多少人？你对这部分人群有何建议？
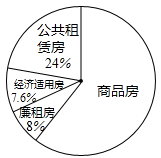
某据信阳市2011年国民经济和社会发展统计公报显示，2011年信阳市新开工的住房有商品房、廉租房、经济适用房和公共租赁房四种类型．老王对这四种新开工的住房套数和比例进行了统计，并将统计结果绘制成下面两幅统计图，请你结合图中所给信息解答下列问题：
（1）求经济适用房的套数，并补全频数分布直方图；
（2）如果2012年、2013年新开工廉租房建设的套数都比前一年增长10%，那么2013年新开工廉租房有多少套？
潼南绿色无公害蔬菜基地有甲、乙两种植户，他们种植了A、B两类蔬菜，两种植户种植的两类蔬菜的种植面积与总收入如下表：
| 种植户 |
种植A类蔬菜面积 （单位：亩） |
种植B类蔬菜面积 （单位：亩） |
总收入 （单位：元） |
| 甲 |
3 |
1 |
12500 |
| 乙 |
2 |
3 |
16500 |
说明：不同种植户种植的同类蔬菜每亩平均收入相等．
⑴ 求A、Ｂ两类蔬菜每亩平均收入各是多少元？
⑵ 某种植户准备租20亩地用来种植A、Ｂ两类蔬菜，为了使总收入不低于63000元，且种植Ａ类蔬菜的面积多于种植Ｂ类蔬菜的面积（两类蔬菜的种植面积均为整数），求该种植户所有租地方案.