(年湖南株洲8分)如图,PQ为圆O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在圆O的上半圆运动(含P、Q两点),以线段AB为边向上作等边三角形ABC.
(1)当线段AB所在的直线与圆O相切时,求△ABC的面积(图1);
(2)设∠AOB=α,当线段AB、与圆O只有一个公共点(即A点)时,求α的范围(图2,直接写出答案);
(3)当线段AB与圆O有两个公共点A、M时,如果AO⊥PM于点N,求CM的长度(图3).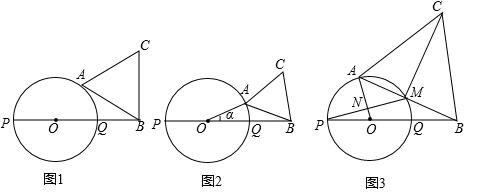
【本小题满分9分】某厂为了丰富大家的业余生活,组织了一次工会活动,准备一次性购买若干钢笔和笔记本(每支钢笔的价格相同,每本笔记本的价格相同)作为奖品.若购买2支钢笔和3本笔记本共需62元,购买5支钢笔和1本笔记本共需90元.
(1)购买一支钢笔和一本笔记本各需多少元?
(2)工会准备购买钢笔和笔记本共80件作奖品,根据规定购买的总费用不超过1100元,则工会最多可以购买多少支钢笔?
【本小题满分9分】某校组织了一次初三科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品.C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图①和图②两幅尚不完整的统计图中.
(1)B班参赛作品有多少件?
(2)请你将图②的统计图补充完整;
(3)通过计算说明,哪个班的获奖率高?
(4)将写有A、B、C、D四个字母的完全相同的卡片放人箱中,从中一次随机抽出两张卡片,求抽到A、B两班的概率.
【本小题满分8分】如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西600的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东450的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
【本小题满分8分】如图,在方格网中已知格点△ABC和点C.
(1)画 和△ABC关于点O成中心对称;
和△ABC关于点O成中心对称;
(2)请在方格网中标出所有使以点A、O、 、D为顶点的四边形是平行四边形的D点.
、D为顶点的四边形是平行四边形的D点.
【本小题满分6分】计算: .
.