（年黑龙江绥化10分）如图，在平面直角坐标系中，已知矩形AOBC的顶点C的坐标是（2，4），动点P从点A出发，沿线段AO向终点O运动，同时动点Q从点B出发，沿线段BC向终点C运动．点P、Q的运动速度均为1个单位，运动时间为t秒．过点P作PE⊥AO交AB于点E．
（1）求直线AB的解析式；
（2）设△PEQ的面积为S，求S与t时间的函数关系，并指出自变量t的取值范围；
（3）在动点P、Q运动的过程中，点H是矩形AOBC内（包括边界）一点，且以B、Q、E、H为顶点的四边形是菱形，直接写出t值和与其对应的点H的坐标．
已知一次函数y1＝x＋b(b为常数)的图象与反比例函数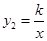
(k为常数，k≠0)的图象相交于点P(3，1)．
(1)求这两个函数的解析式；
(2)当x＞3时，试判断y1与y2的大小，并说明理由．
如下图，在梯形OABC中，OC∥AB，OA＝CB，点O为坐标原点，且A(2，－3)，C(0，2)．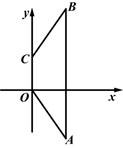
(1)求过点B的双曲线的解析式．
(2)若将等腰梯形OABC向右平移5个单位，问：平移后的点C是否落在(1)中的双曲线上？并简述理由．
如下图，已知直线y＝－x＋3与反比例函数的图象交于点P(2，1)，求反比例函数的关系式．
如下图，已知反比例函数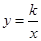
(k≠0)的图象经过点(
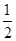，8)，直线y＝－x＋b经过反比例函数图象上的点Q(4，m)，求反比例函数和直线的解析式．
已知y与x成反比例，当x＝2时，y＝3．
（1）求函数解析式；
（2）当
时，求y的值．