如下图,在梯形OABC中,OC∥AB,OA=CB,点O为坐标原点,且A(2,-3),C(0,2).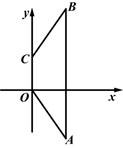
(1)求过点B的双曲线的解析式.
(2)若将等腰梯形OABC向右平移5个单位,问:平移后的点C是否落在(1)中的双曲线上?并简述理由.
小明想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:
如示意图,小明边移动边观察,发现站到点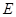 处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点
处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点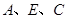 在同一直线上).
在同一直线上).
已知小明的身高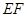 是1.7m,请你帮小明求出楼高
是1.7m,请你帮小明求出楼高 (结果精确到0.1m).
(结果精确到0.1m).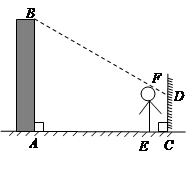
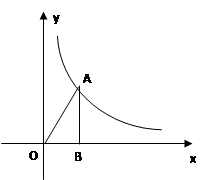
第一象限内的点A在某一反比例函数的图象上,过A作AB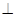 x轴,垂足为B,连接AO,已知△AOB的面积为4.
x轴,垂足为B,连接AO,已知△AOB的面积为4. ⑴求反比例函数的解析式
⑵若点A的纵坐标为4,过点A的直线与x轴交于P(不与点B、O重合),且以A、P、B为顶点的三角形与△AOB相似,写出符合条件的点P的坐标.
如图,矩形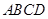 中,
中,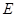 为
为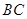 上一点,
上一点,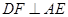 于
于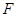 .若
.若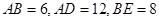 ,求:
,求: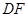 的长,以及四边形DCEF的面积。
的长,以及四边形DCEF的面积。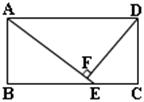
在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上。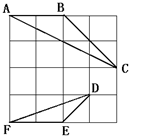
(1)填空:∠ABC=°,BC=
(2)判断△ABC与△DEF是否相似,并说明理由.
(3)请在图中再画一个和△ABC相似但相似比不为1的格点三角形.
解方程:(4+4=8分)(1)
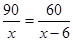
(2)
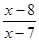 —
—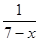 =8
=8