（2014年湖北襄阳12分）如图，在平面直角坐标系中，矩形OCDE的三个顶点分别是C（3，0），D（3，4），E（0，4）．点A在DE上，以A为顶点的抛物线过点C，且对称轴x=1交x轴于点B．连接EC，AC．点P，Q为动点，设运动时间为t秒．
（1）填空：点A坐标为 ；抛物线的解析式为 ．
（2）在图1中，若点P在线段OC上从点O向点C以1个单位/秒的速度运动，同时，点Q在线段CE上从点C向点E以2个单位/秒的速度运动，当一个点到达终点时，另一个点随之停止运动．当t为何值时，△PCQ为直角三角形？
（3）在图2中，若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动，过点P做PF⊥AB，交AC于点F，过点F作FG⊥AD于点G，交抛物线于点Q，连接AQ，CQ．当t为何值时，△ACQ的面积最大？最大值是多少？
已知：如图，直线y=﹣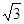
x+4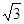与x轴相交于点A，与直线y=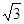x交于点P．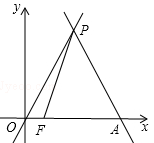
（1）求点P的坐标．
（2）动点F从原点O出发，以每秒1个单位的速度在线段OA上向点A作匀速运动，连接PF，设运动时间为t秒，△PFA的面积为S，求出S关于t的函数关系式．
（3）若点M是y轴上任意一点，点N是坐标平面内任意一点，若以O、M、N、P为顶点的四边形是平行四边形，请直接写出点N的坐标．
提出问题：如图①，在正方形ABCD中，点P，F分别在边BC、AB上，若AP⊥DF于点H，则AP=DF．类比探究：
（1）如图②，在正方形ABCD中，点P、F．、G分别在边BC、AB、AD上，若GP⊥DF于点H，探究线段GP与DF的数量关系，并说明理由；
（2）如图③，在正方形ABCD中，点P、F、G分别在边BC、AB、AD上，GP⊥DF于点H，将线段PG绕点P逆时针旋转90°得到线段PE，连结EF，若四边形DFEP为菱形，探究DG和PC的数量关系，并说明理由．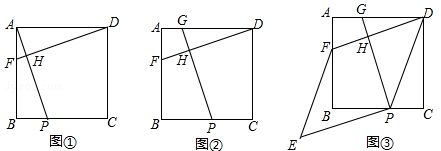
某学校开展“科技创新大赛”活动，设计遥控车沿直线轨道做匀速直线运动
的模型．现在甲、乙两车同时分别从不同起点A，B出发，沿同一轨道到达C处．设t后甲、乙两遥控车与B处的距离分别为d1，d2，且d1，d2与t的函数关系如图，若甲的速度是乙的速度的1．5倍，试根据图象解决下列问题：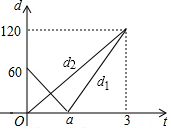
（1）填空：乙的速度是米/分；
（2）写出d1与t的函数关系式；
（3）若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰，试探求什么时间两遥控车的信号不会产生相互干扰？
某公司招聘人才，共有50人进入复试．对应聘者分别进行阅读能力、思维能力和表达能力三项侧试，甲、乙两人的成绩如表（单位：分）：
| 阅读 |
思维 |
表达 |
|
| 甲 |
93 |
86 |
73 |
| 乙 |
95 |
81 |
79 |
（1）根据实际需要，公司将阅读、思维和表达能力三项测试得分按3：5：2确定每人的最后成绩，若按此成绩在甲、乙两人中录用一人，谁将被录用？
（2）公司按照（1）中的成绩计算方法，将每位应聘者的最后成绩绘制成如图所示的频数分布直方图，请计算此次参加复试人员的平均分．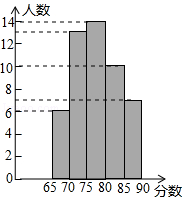
如图，四边形ABCD是矩形，∠EDC=∠CAB，∠DEC=90°．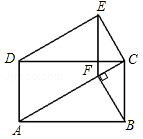
（1）求证：AC∥DE；
（2）过点B作BF⊥AC于点F，连接EF，试判别四边形BCEF的形状，并说明理由．