已知：如图，直线y=﹣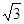
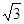x+4与x轴相交于点A，与直线y=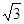x交于点P．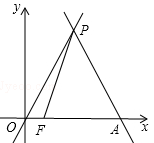
（1）求点P的坐标．
（2）动点F从原点O出发，以每秒1个单位的速度在线段OA上向点A作匀速运动，连接PF，设运动时间为t秒，△PFA的面积为S，求出S关于t的函数关系式．
（3）若点M是y轴上任意一点，点N是坐标平面内任意一点，若以O、M、N、P为顶点的四边形是平行四边形，请直接写出点N的坐标．
如图，将平行四边形ABCD沿对角线BD进行折叠，折叠后点C落在点F处，DF交AB于点E．
（1）求证：
；
（2）判断AF与BD是否平行，并说明理由．
如图，把△EFP按图所示的方式放置在菱形ABCD中，使得顶点E、F、P分别在线段AB、AD、AC上.已知EP=FP=
，EF=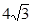
，∠BAD=60°，且AB
.
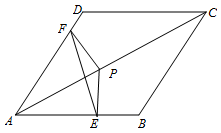
（1）求∠EPF的大小；
（2）若AP=6，求AE+AF的值；
（3）若△EFP的三个顶点E、F、P分别在线段AB、AD、AC上运动，请直接写出AP长的最大值和最小值.
如图，在边长为4的正方形ABCD中，请画出以A为一个顶点，另外两个顶点在正方形ABCD的边上，且含边长为3的所有大小不同的等腰三角形．（要求：只要画出示意图，并在所画等腰三角形长为3的边上标注数字3）
如图，已知一条直线过点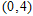
，且与抛物线
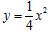交于A，B两点，其中点A的横坐标是
．
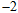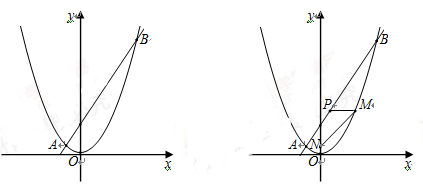
（1）求这条直线的函数关系式及点B的坐标；
（2）在x轴上是否存在点C，使得△ABC是直角三角形？若存在，求出点C的坐标；若不存在，请说明理由；
（3） 过线段AB上一点P，作PM //x轴，交抛物线于点M，点M在第一象限，点N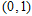
，当点M的横坐标为何值时，
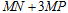的长度最大？最大值是多少？
已知如图，在平面直角坐标系
中，直线
与
轴、
轴分别交于A，B两点，P是直线AB上一动点，⊙
的半径为1．
（1）判断原点O与⊙的位置关系，并说明理由；
（2）当⊙过点B时，求⊙被轴所截得的劣弧的长；
（3）当⊙与轴相切时，求出切点的坐标．