已知如图,在平面直角坐标系 中,直线
中,直线 与
与 轴、
轴、 轴分别交于A,B两点,P是直线AB上一动点,⊙
轴分别交于A,B两点,P是直线AB上一动点,⊙ 的半径为1.
的半径为1.
(1)判断原点O与⊙ 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)当⊙ 过点B时,求⊙
过点B时,求⊙ 被
被 轴所截得的劣弧的长;
轴所截得的劣弧的长;
(3)当⊙ 与
与 轴相切时,求出切点的坐标.
轴相切时,求出切点的坐标.
如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E.
(1)求证:BD=BE;
(2)若ÐDBC=30°,BO=4,求四边形ABED的面积.
如图,在梯形ABCD中,AD∥BC,AB=" DC" =AD,BD⊥CD.设∠DBC=x°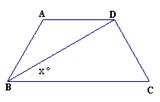
(1)你能用x表示图中的哪些角?(写出3个即可)
(2)列一个关于x的方程,并求这个方程的解。
(1)如图,在6×6的网格中,请你画出一个格点正方形ABCD,使它的面积是10;
(2)如图,A、B是4×5的网格中的格点,网格中每个小正方形的边长都是单位1,请在图中清晰地标出使以A、B、C为顶点的三角形是等腰三角形的所有格点C的位置。
有一块形状如图所示的玻璃,其中AD∥BC,不小心把DEF部分打碎,现在只测得AB=30cm,BC=70cm,∠B=600,∠C=1500,请根据测得的数据求出AD的长.
如图, 中,
中, ,
, 垂直平分
垂直平分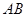 ,
,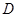 为垂足交
为垂足交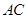 于
于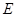 .
.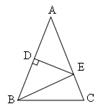
(1)若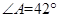 ,求
,求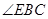 的度数;
的度数;
(2)若 ,
,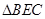 的周长是
的周长是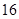 ,求
,求 的周长.
的周长.