(年四川雅安12分)如图,直线y=﹣3x﹣3与x轴、y轴分别相交于点A、C,经过点C且对称轴为x=1的抛物线y=ax2+bx+c与x轴相交于A、B两点.
(1)试求点A、C的坐标;
(2)求抛物线的解析式;
(3)若点M在线段AB上以每秒1个单位长度的速度由点B向点A运动,同时,点N在线段OC上以相同的速度由点O向点C运动(当其中一点到达终点时,另一点也随之停止运动),又PN∥x轴,交AC于P,问在运动过程中,线段PM的长度是否存在最小值?若有,试求出最小值;若无,请说明理由.
(本题7分) 如图,四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE =CF.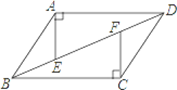
求证:(1)△ADE ≌△CBF;
(2)AB=CD.
(每小题4分,共8分)计算:
(1)已知:(x+2)2=25,求x;
(2)计算: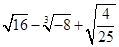 .
.
如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE,等边△BCF。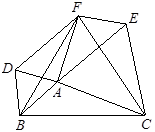
(1)求证:四边形DAEF平行四边形;
(2)(2)探究下列问题:(只填满足的条件,不需要证明)
①当∠A=时,四边形DAEF是矩形;
②当△ABC满足条件时,四边形DAEF是菱形;
③当△ABC满足条件时;以D、A、E、F为顶点的四边形不存在
如图,梯形ABCD中,AD∥BC,对角线BD的垂直平分线与两底AD、BC分别交于点E、F,判断四边形BEDF的形状并说明理由。
已知:如图,四边形ABCD是矩形(AD>AB),点E在BC上,且AE=AD,DF⊥AE,垂足为F。请探求DF与AB有何数量关系?写出你所得到的结论并给予证明。