（年广东广州14分）已知平面直角坐标系中两定点A（﹣1，0）、B（4，0），抛物线y=ax2+bx﹣2（a≠0）过点A，B，顶点为C，点P（m，n）（n＜0）为抛物线上一点．
（1）求抛物线的解析式和顶点C的坐标；
（2）当∠APB为钝角时，求m的取值范围；
（3）若m＞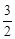
，当∠APB为直角时，将该抛物线向左或向右平移t（0＜t＜
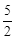）个单位，点C、P平移后对应的点分别记为C′、P′，是否存在t，使得首尾依次连接A、B、P′、C′所构成的多边形的周长最短？若存在，求t的值并说明抛物线平移的方向；若不存在，请说明理由．
.
后得到的△AB1C1，并求出CC1的长.
.