已知，△ABC是边长为4cm的等边三角形，点P，Q分别从顶点A，B同时出发，沿线段AB，BC运动，且它们的速度均为1cm/s．当点P到达点B时，P、Q两点停止运动．设点P的运动时间为t（s）．
（1）如图1，连接AQ、CP，相交于点M，则点P，Q在运动的过程中，∠CMQ会变化吗？若变化，则说明理由；若不变，请求出它的度数．
（2）如图2，当t为何值时，△PBQ是直角三角形？
（3）如图3，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，请直接写出∠CMQ度数．
如图1，在平面直角坐标系中，抛物线
交x轴于A（﹣1，0）和B（5，0）两点，交y轴于点C，点D是线段OB上一动点，连接CD，将线段CD绕点D顺时针旋转90°得到线段DE，过点E作直线l⊥x轴于H，过点C作CF⊥l于F．
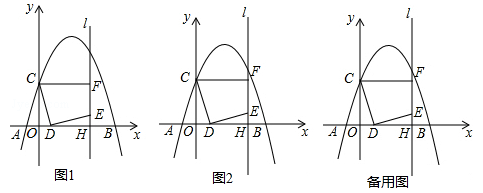
（1）求抛物线解析式；
（2）如图2，当点F恰好在抛物线上时，求线段OD的长；
（3）在（2）的条件下：
①连接DF，求tan∠FDE的值；
②试探究在直线l上，是否存在点G，使∠EDG=45°？若存在，请直接写出点G的坐标；若不存在，请说明理由．
如图1，△ABC和△AED都是等腰直角三角形，∠BAC=∠EAD=90°，点B在线段AE上，点C在线段AD上．
（1）请直接写出线段BE与线段CD的关系：；
（2）如图2，将图1中的△ABC绕点A顺时针旋转角α（0＜α＜360°），
①（1）中的结论是否成立？若成立，请利用图2证明；若不成立，请说明理由；
②当AC=
ED时，探究在△ABC旋转的过程中，是否存在这样的角α，使以A、B、C、D四点为顶点的四边形是平行四边形？若存在，请直接写出角α的度数；若不存在，请说明理由．
盘锦红海滩景区门票价格80元/人，景区为吸引游客，对门票价格进行动态管理，非节假日打a折，节假日期间，10人以下（包括10人）不打折，10人以上超过10人的部分打b折，设游客为x人，门票费用为y元，非节假日门票费用
（元）及节假日门票费用
（元）与游客x（人）之间的函数关系如图所示．
（1）a=，b=；
（2）直接写出、与x之间的函数关系式；
（3）导游小王6月10日（非节假日）带A旅游团，6月20日（端午节）带B旅游团到红海滩景区旅游，两团共计50人，两次共付门票费用3040元，求A、B两个旅游团各多少人？
如图1，AB为⊙O的直径，点P是直径AB上任意一点，过点P作弦CD⊥AB，垂足为P，过点B的直线与线段AD的延长线交于点F，且∠F=∠ABC．
（1）若CD=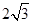
，BP=4，求⊙O的半径；
（2）求证：直线BF是⊙O的切线；
（3）当点P与点O重合时，过点A作⊙O的切线交线段BC的延长线于点E，在其它条件不变的情况下，判断四边形AEBF是什么特殊的四边形？请在图2中补全图象并证明你的结论．
如图所示，小明家小区空地上有两颗笔直的树CD、EF．一天，他在A处测得树顶D的仰角∠DAC=30°，在B处测得树顶F的仰角∠FBE=45°，线段BF恰好经过树顶D．已知A、B两处的距离为2米，两棵树之间的距离CE=3米，A．B、C、E四点在一条直线上，求树EF的高度．（
≈1.7，
≈1.4，结果保留一位小数）