如图1，在平面直角坐标系中，抛物线
交x轴于A（﹣1，0）和B（5，0）两点，交y轴于点C，点D是线段OB上一动点，连接CD，将线段CD绕点D顺时针旋转90°得到线段DE，过点E作直线l⊥x轴于H，过点C作CF⊥l于F．
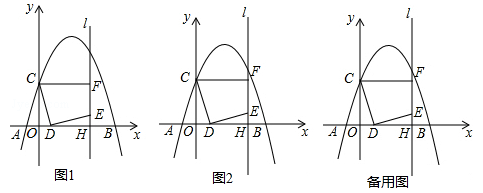
（1）求抛物线解析式；
（2）如图2，当点F恰好在抛物线上时，求线段OD的长；
（3）在（2）的条件下：
①连接DF，求tan∠FDE的值；
②试探究在直线l上，是否存在点G，使∠EDG=45°？若存在，请直接写出点G的坐标；若不存在，请说明理由．
如图1，在平面直角坐标系中，以坐标原点O为圆心的⊙O的半径为
，直线
与坐标轴分别交于A、C两点，点B的坐标为(4,1)，⊙B与x轴相切于点M。
（1）求点A的坐标及∠CAO的度数；
（2）⊙B以每秒1个单位长度的速度沿x轴负方向平移，同时，若直线
绕点A顺时针匀速旋转，当⊙B第一次与⊙O相切时，直线也恰好与⊙B第一次相切，见图（2）求B1的坐标以及直线AC绕点A每秒旋转多少度？
（3）若直线不动，⊙B沿x轴负方向平移过程中，能否与⊙O与直线同时相切。若相切，说明理由。
如图，线段AB经过圆心O，交⊙O于点A、C，∠BAD＝∠B＝30°,边BD交圆于点D。
（1）求证BD是⊙O的切线。
（2）若⊙O的半径为2，求弦AD的长。
上海市顺风旅行社为吸引市民组团去雁荡山风景区旅游，推出了如下收费标准：
某单位组织员工去雁荡山风景区旅游，共支付给顺风旅游社旅游费用27000元，请问该单位这次共有多少员工去雁荡山风景区旅游？
如图，已知△ABC的顶点A、B、C的坐标分别是A（－1，－l），B（－5，－4），C（－5，－l）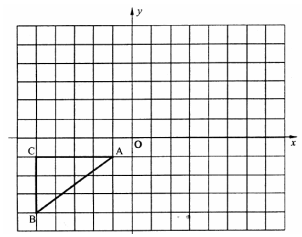
（1）作出△ABC关于点O（0，0）中心对称的图形△A1B1C1，并直接写出顶点A1的坐标．
（2）将△ABC绕原点O按顺时针方向旋转90°后得到△A2B2C2，画出△A2B2C2，并直接写出顶点A2、的坐标．
解方程：