如图1,在平面直角坐标系中,以坐标原点O为圆心的⊙O的半径为 ,直线
,直线 与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M。
与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M。
(1)求点A的坐标及∠CAO的度数;
(2)⊙B以每秒1个单位长度的速度沿x轴负方向平移,同时,若直线 绕点A顺时针匀速旋转,当⊙B第一次与⊙O相切时,直线
绕点A顺时针匀速旋转,当⊙B第一次与⊙O相切时,直线 也恰好与⊙B第一次相切,见图(2)求B1的坐标以及直线AC绕点A每秒旋转多少度?
也恰好与⊙B第一次相切,见图(2)求B1的坐标以及直线AC绕点A每秒旋转多少度?
(3)若直线 不动,⊙B沿x轴负方向平移过程中,能否与⊙O与直线
不动,⊙B沿x轴负方向平移过程中,能否与⊙O与直线 同时相切。若相切,说明理由。
同时相切。若相切,说明理由。

解方程.
(1)3(x+1)﹣2(x+2)=2x+3
(2)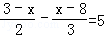
(3)
(4) +
+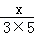 +
+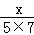 +…+
+…+ =2014.
=2014.
如图,已知数轴上点A表示的数为6,B是数轴上在A左侧的一点,且A,B两点间的距离为10.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)数轴上点B表示的数是 ,点P表示的数是 (用含t的代数式表示);
(2)动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点P、Q时出发.求:
①当点P运动多少秒时,点P与点Q相遇?
②当点P运动多少秒时,点P与点Q间的距离为8个单位长度?
在端午节期间,小明、小亮等同学随家人一同到泰山游玩,已知:票价成人35元一张,学生按成人票5折优惠,团体票16人(含16人)以上一律按成人票6折优惠.下面是购买门票时,小明与他爸爸的对话.
爸爸:大人门票每张35元,学生门票对折优惠,我们共有12人,共需350元.
小明:爸爸,让我算一算,换一种方式买票是否更省钱.
问题(1)小明他们一共去了几个成年人?几个学生?
(2)请你帮小明算一算,哪种方式买票更省钱?并说明理由?
如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=acm,其它条件不变,你能猜想MN的长度吗?并说明理由.
如图,平面上有四个点A、B、C、D,根据下列语句画图.
(1)画直线AB;
(2)作射线BC;
(3)画线段CD;
(4)连接AD,并将其反向延长至E,使DE=2AD;
(5)找到一点F,使点F到A、B、C、D四点距离和最短.