如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.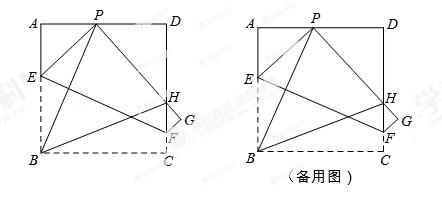
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;
(3)设AP为x,四边形EFGP的面积为S,求出S与x的函数关系式,试问S是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
如图1,在△ABC中,AB=BC=5,AC="6." △ECD是△ABC沿BC方向平移得到的,连接AE.AC和BE相交于点O.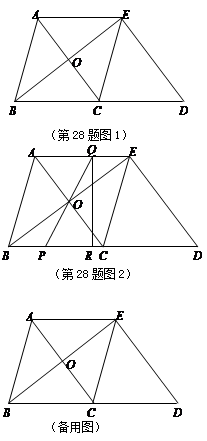
(1)判断四边形ABCE是怎样的四边形,说明理由;
(2)如图2,P是线段BC上一动点(图2),(不与点B、C重合),连接PO并延长交线段AE于点Q,QR⊥BD,垂足为点R.
①四边形PQED的面积是否随点P的运动而发生变化?
若变化,请说明理由;若不变,求出四边形PQED的面积;
②当线段BP的长为何值时,△PQR与△BOC相似?
(1)探究新知: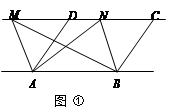
①如图,已知AD∥BC,AD=BC,点M,N是直线CD上任意两点.试判断△ABM与△ABN的面积是否相等。
②如图,已知AD∥BE,AD=BE,AB∥CD∥EF,点M是直线CD上任一点,点G是直线EF上任一点.试判断△ABM与△ABG的面积是否相等,并说明理由.
(2)结论应用:
如图③,抛物线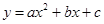 的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线
的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线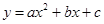 上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等? 若存在,请求出此时点E的坐标,若不存在,请说明理由.
上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等? 若存在,请求出此时点E的坐标,若不存在,请说明理由.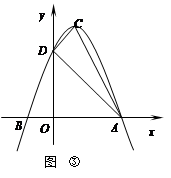
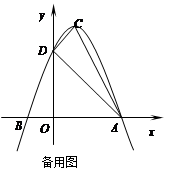

张先生前年在美美家园住宅小区订购了一套住房,图纸如图所示。已知:①该住房的价格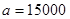 元/平方米;②楼层的电梯、楼梯及门厅前室面积由两户购房者平均负担;③每户配置车库16平方米,每平方米以6000元计算;
元/平方米;②楼层的电梯、楼梯及门厅前室面积由两户购房者平均负担;③每户配置车库16平方米,每平方米以6000元计算;
根据以上提供的信息和数据计算:
(1)张先生这次购房总共应付款多少元?
(2)若经过两年,该住房价格变为21600元/平方米,那么该小区房价的年平均增长率为多少?
(3)张先生打算对室内进行装修,甲、乙两公司推出不同的优惠方案:在甲公司累计购买10000元材料后,再购买的材料按原价的90%收费;在乙公司累计购买5000元材料后,再购买的材料按原价的95%收费.张先生怎样选择能获得更大优惠?
如图,直线y=kx-1与x轴、y轴分别交与B、C两点,tan∠OCB=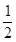 .
.
(1)求B点的坐标和k的值;
(2)若点A(x,y)是第一象限内的直线y=kx-1上的一个动点.当点A运动过程中,试写出△AOB的面积S与x的函数关系式;
(3)探索:
①当点A运动到什么位置时,△AOB的面积是 ;
;
②在①成立的情况下,x轴上是否存在一点P,使△POA是等腰三角形.若存在,请写出满足条件的所有P点的坐标;若不存在,请说明理由.
(本小题满分8分)按右图所示的流程,输入一个数据x,根据y与x的关系式就输出一个数据y,这样可以将一组数据变换成另一组新的数据,要使任意一组都在20~100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求:
(a)新数据都在60~100(含60和100)之间;
(b)新数据之间的大小关系与原数据之间的大小关系一致,即原数据大的对应的新数据也较大。
(1)若y与x的关系是y=x+p(100-x),请说明:当p=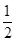 时,这种变换满足上述两个要求;
时,这种变换满足上述两个要求;
(2)若按关系式y=a(x-h)2+k (a>0)将数据进行变换,请写出一个满足上述要求的这种关系式。(不要求对关系式符合题意作说明,但要写出关系式得出的主要过程)