(年山东日照14分)如图1,在菱形OABC中,已知OA=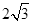 ,∠AOC=60°,抛物线y=ax2+bx+c(a≠0)经过O,C,B三点.
,∠AOC=60°,抛物线y=ax2+bx+c(a≠0)经过O,C,B三点.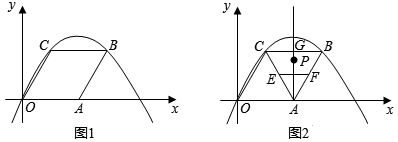
(1)求出点B、C的坐标并求抛物线的解析式.
(2)如图2,点E是AC的中点,点F是AB的中点,直线AG垂直BC于点G,点P在直线AG上.
①当OP+PC的最小值时,求出点P的坐标;
②在①的条件下,连接PE、PF、EF得△PEF,问在抛物线上是否存在点M,使得以M,B,C为顶点的三角形与△PEF相似?若存在,请求出点M的坐标;若不存在,请说明理由.
有一个数学活动,其具体操作过程是:
第一步:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开
(如图1);
第二步:再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN(如图2).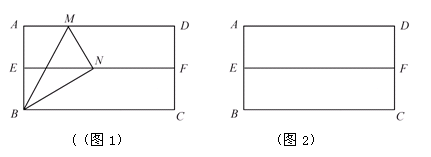
请解答以下问题:如图2,若延长MN交线段BC于P,△BMP是什么三角形?请证明你的结论.
在图2中,若AB=a,BC=b,a、b满足什么关系,才能在矩形纸片ABCD上剪出符合(1)中结论的三角形纸片BMP
如图,过点P(2,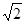 )作
)作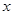 轴的平行线交
轴的平行线交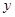 轴于点
轴于点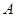 ,交双曲线
,交双曲线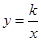 (
(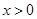 )于点
)于点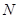 ,作
,作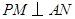 交双曲线
交双曲线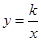 (
(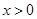 )于点
)于点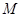 ,连结
,连结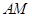 .已 知
.已 知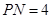
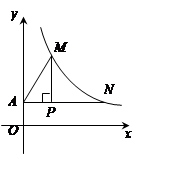
求
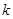 的值
的值设直线MN解析式为
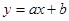 ,
,
求不等式 ≥
≥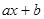 的解集;
的解集;
有一人患了流感,经过两轮传染后共有81人患了流感,每轮传染中平均一个人传染了几个人
如图,在 ABCD的
ABCD的 各边AB、BC、CD、DA上,分别取点K、L、M、N,使A
各边AB、BC、CD、DA上,分别取点K、L、M、N,使A K=CM、BL=DN,求证:四边形KLMN为平行四边形。
K=CM、BL=DN,求证:四边形KLMN为平行四边形。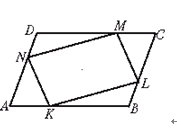
如图,要在一块形状为直角三角形(∠C为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮上画出一个半圆,使它的圆心在线段AC上,且与AB、BC都相切.请你用直尺和圆规画出来(要求用尺规作图,保留作图痕迹,不要求写作法).