(年浙江义乌12分)如图,直角梯形ABCO的两边OA,OC在坐标轴的正半轴上,BC∥x轴,OA=OC=4,以直线x=1为对称轴的抛物线过A,B,C三点.
(1)求该抛物线线的函数解析式.
(2)已知直线l的解析式为 ,它与x轴的交于点G,在梯形ABCO的一边上取点P.
,它与x轴的交于点G,在梯形ABCO的一边上取点P.
①当m=0时,如图1,点P是抛物线对称轴与BC的交点,过点P作PH⊥直线l于点H,连结OP,试求△OPH的面积.
②当 时,过P点分别作x轴、直线l的垂线,垂足为点E,F. 是否存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
时,过P点分别作x轴、直线l的垂线,垂足为点E,F. 是否存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.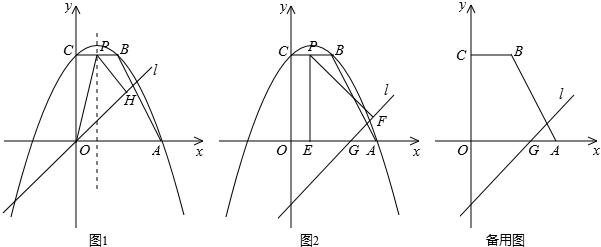
如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.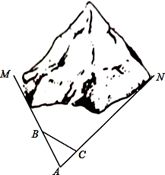
如图,是一块三角形土地,它的底边BC长为100米,高AH为80米,某单位要沿着底边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上,若大楼的宽是40米,求这个矩形的面积。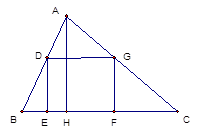
已知:直角梯形 中,
中, ∥
∥ ,∠
,∠ =
= ,以
,以 为直径的圆
为直径的圆 交
交 于点
于点 、
、 ,连结
,连结 、
、 、
、 .
.
(1)在不添加其他字母和线的前提下,直接写出图1中的两对相似三角形:
_____________________,______________________ ;
(2)直角梯形 中,以
中,以 为坐标原点,
为坐标原点, 在
在 轴正半轴上建立直角坐标系(如图2),若抛物线
轴正半轴上建立直角坐标系(如图2),若抛物线 经过点
经过点 、
、 、
、 ,且
,且 为抛物线的顶点.
为抛物线的顶点.
①写出顶点 的坐标(用含
的坐标(用含 的代数式表示)___________;
的代数式表示)___________;
②求抛物线的解析式;
③在 轴下方的抛物线上是否存在这样的点
轴下方的抛物线上是否存在这样的点 ,过点
,过点 作
作 ⊥
⊥ 轴于点
轴于点 ,使得以点
,使得以点 、
、 、
、 为顶点的三角形与△
为顶点的三角形与△ 相似?
相似?
如图1,△ABC中,BC=25,BC边上的高为20,将AB,AC分别n等分,连接两边对应的等分点,以这些连接线为一边做矩形,使这些矩形的边B1C1,B2C2,B3C3……的对应边分别为 B2C2,B3C3,B4C4……
(1)若n=5,如图2,求B3C3为一边的矩形的面积;
(2)若n=5,求所有矩形的面积和;
(3)当分为n等分时,你能用含有n的表达式表示所有矩形的面积和吗?
小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: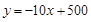 ,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的80%.
,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的80%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润为2000元,那么小明每月的成本需要多少元?(成本=进价×销售量)