（年广东梅州11分）如图，已知抛物线
与x轴的交点为A、D（A在D的右侧），与y轴的交点为C.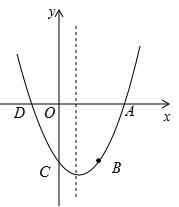
（1）直接写出A、D、C三点的坐标；
（2）在抛物线的对称轴上找一点M，使得MD+MC的值最小，并求出点M的坐标；
（3）设点C关于抛物线对称的对称点为B，在抛物线上是否存在点P，使得以A、B、C、P四点为顶点的四边形为梯形？若存在，求出点P的坐标；若不存在，请说明理由.
（1）半径为R的圆的面积恰好是半径为5与半径为2的两个圆面积之差，求R的值。
（2）某次商品交易会上，所有参加会议的商家之间都签订了一份合同，共签订合同36份，求共有多少商家参加了交易会？
若x=1是方程mx2＋3x＋n=0的根，求（m－n）2＋4mn的值。
用适当的方法解下列方程：
（1）
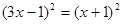
（2）
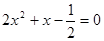
如图，△ABC是一块锐角三角形余料，其中BC=12cm，高AD=8cm，现在要把它裁成一块正方形材料备用，使正方形的一边QM在BC上，其余两个顶点P，N分别在AB，AC上，问这块正方形材料的边长是多少？
如图，□ABCD中，E是CD的延长线上一点，BE与AD交于点F，
。
（1）求证：△ABF∽△CEB;
（2）若△DEF的面积为2，求□ABCD的面积。