（年湖北天门学业12分）如图，已知二次函数的图象过点A（0，﹣3），B（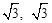
），对称轴为直线
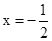，点P是抛物线上的一动点，过点P分别作PM⊥x轴于点M，PN⊥y轴于点N，在四边形PMON上分别截取PC=
MP，MD=OM，OE=ON，NF=NP．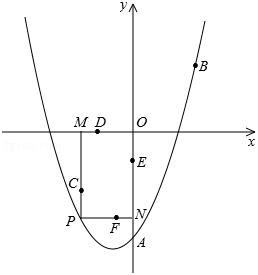
（1）求此二次函数的解析式；
（2）求证：以C、D、E、F为顶点的四边形CDEF是平行四边形；
（3）在抛物线上是否存在这样的点P，使四边形CDEF为矩形？若存在，请求出所有符合条件的P点坐标；若不存在，请说明理由．
列方程或方程组解应用题：
中国2010年上海世博会第三期预售平日门票分为普通票和优惠票，其中普通票每张150元人民币，优惠票每张90元人民币．某日一售票点共售出1000张门票，总收入12.6万元人民币．那么，这一售票点当天售出的普通票和优惠票各多少张？
注：优惠票的适用对象包括残疾人士、老年人（1950年12月31日前出生的）、学生、身高超过1.20米的儿童、现役军人．
如图，一次函数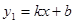
的图象与反比例函数
的图象相交于A、B两点．求出这两个函数的解析式；
结合函数的图象回答：当自变量x的取值范围满足什么条件时，
？
已知：如图，□ABCD中，点E是AD的中点，延长CE交BA的延长线于点F．
求证：AB=AF．
如图1，正方形ABCD和正方形QMNP，∠M =∠B，M是正方形ABCD的对称中心，MN交AB于F，QM交AD于E．求证：ME = MF．
如图2，若将原题中的“正方形”改为“菱形”，其他条件不变，探索线段ME与线段MF的关系，并加以证明．
如图3，若将原题中的“正方形”改为“矩形”，且AB = mBC，其他条件不变，探索线段ME与线段MF的关系，并说明理由．
根据前面的探索和图4，你能否将本题推广到一般的平行四边形情况？若能，写出推广命题；若不能，请说明理由．
如图已知AB是
的切线，切点为
交于点
过点
作
交
于点
求证：
；若
的半径为4，求CD的长；求阴影部分的面积。
