(年湖南岳阳10分)如图,抛物线经过点A(1,0),B(5,0),C(0, )三点,设点E(x,y)是抛物线上一动点,且在x轴下方,四边形OEBF是以OB为对角线的平行四边形.
)三点,设点E(x,y)是抛物线上一动点,且在x轴下方,四边形OEBF是以OB为对角线的平行四边形.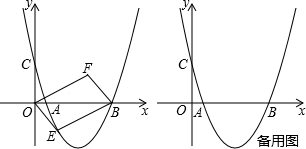
(1)求抛物线的解析式;
(2)当点E(x,y)运动时,试求平行四边形OEBF的面积S与x之间的函数关系式,并求出面积S的最大值?
(3)是否存在这样的点E,使平行四边形OEBF为正方形?若存在,求E点,F点的坐标;若不存在,请说明理由.
解不等式(组)并将解集在数轴上表示出来.
(1)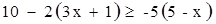 (2)
(2)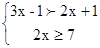
解方程组(1)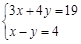 (2)
(2)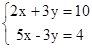
解方程 (1) 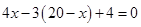 (2)
(2)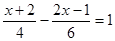
如图,一次函数y1=ax+2与反比例函数y2= 的图象交于点A(4,m)和B(-8,-2),与y轴交于点C,与x轴交于点D.
的图象交于点A(4,m)和B(-8,-2),与y轴交于点C,与x轴交于点D.
(1)求a、k的值;
(2)过点A作AE⊥x轴于点E,若P为反比例函数图象的位于第一象限部分上的一点,且直线OP分△ADE所得的两部分面积之比为2∶7.请求出所有符合条件的点P的坐标;
(3)在(2)的条件下,请在x轴上找一点Q,使得△PQC的周长最小,并求出点Q的坐标.
进入防汛期后,某地对河堤进行了加固.该地驻军在河堤加固的工程中出色完成了任务.这是记者与驻军工程指挥官的一段对话:
记者:听说你们是用9天完成4800米长的大坝加固任务的?
指挥官:对!我们加固600米后,采用新的加固模式,这样每天加固长度是原来的2倍……
通过这段对话,请你求出该地驻军原来每天加固的米数.