（年江苏苏州10分）如图，二次函数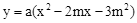
（其中a，m是常数，且a>0，m>0）的图象与x轴分别交于点A，B（点A位于点B的左侧），与y轴交于点C(0，－3)，点D在二次函数的图象上，CD∥AB，连接AD．过点A作射线AE交二次函数的图象于点E，AB平分∠DAE．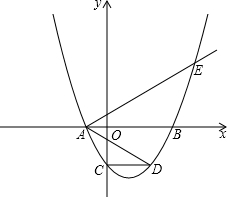
（1）用含m的代数式表示a；
（2）)求证：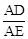
为定值；
（3）设该二次函数图象的顶点为F．探索：在x轴的负半轴上是否存在点G，连接CF，以线段GF、AD、AE的长度为三边长的三角形是直角三角形？如果存在，只要找出一个满足要求的点G即可，并用含m的代数式表示该点的横坐标；如果不存在，请说明理由．
长岭中心中学现要从甲、乙两位男生和丙、丁两位女生中，选派两位同学分别作为①号选手和②号选手代表学校参加全镇汉字听写大赛．
（1）请用树状图或列表法列举出各种可能选派的结果；
（2）求恰好选派一男一女两位同学参赛的概率．
广水市为了改善全市中、小学办学条件，计划集中采购一批电子白板和投影机．已知购买2块电子白板比购买3台投影机多4000元，购买4块电子白板和3台投影机共需44000元．问购买一块电子白板和一台投影机各需要多少元？
解不等式组：
，
为鼓励大学毕业生自主创业，某市政府出台了相关政策：由政府协调，本市企业按成本价提供产品给大学毕业生自主销售，成本价与出厂价之间的差价由政府承担．李明按照相关政策投资销售本市生产的一种新型节能灯．已知这种节能灯的成本价为每件10元，出厂价为每件12元，每月销售量y（件）与销售单价x（元）之间的关系近似满足一次函数：y=﹣10x+500．
（1）李明在开始创业的第一个月将销售单价定为20元，那么政府这个月为他承担的总差价为多少元？
（2）设李明获得的利润为w（元），当销售单价定为多少元时，每月可获得最大利润？
（3）物价部门规定，这种节能灯的销售单价不得高于25元．如果李明想要每月获得的利润不低于3000元，那么政府为他承担的总差价最少为多少元？
已知，如图，A（0．8），B（4，0），D是AB的中点，过D点作直线与△AOB的一边交于点E，直线DE截△ABO得到的小三角形与△ABO相似，求满足题意的所有E点的坐标．