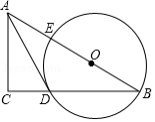
(年江苏扬州12分)已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.
(1)如图1,已知折痕与边BC交于点O,连接AP,OP,OA.
①求证:△OCP∽△PDA;
②若△OCP与△PDA的面积比为1:4,求边AB的长;
(2)若图1中的点P恰巧是CD边的中点,求∠OAB的度数;
(3)如图2,在(1)条件下,擦去折痕AO、线段OP,连结BP. 动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E. 试问当点M,N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求线段EF的长度.
在第23个世界读书日前夕,我市某中学为了解本校学生的每周课外阅读时间(用 表示,单位:小时),采用随机抽样的方法进行问卷调查,调查结果按 , , , 分为四个等级,并依次用 , , , 表示,根据调查结果统计的数据,绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
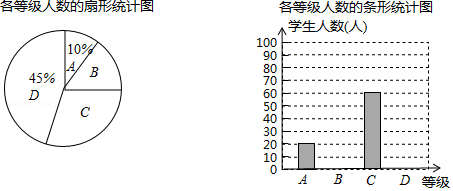
(1)求本次调查的学生人数;
(2)求扇形统计图中等级 所在扇形的圆心角度数,并把条形统计图补充完整;
(3)若该校共有学生1200人,试估计每周课外阅读时间满足 的人数.
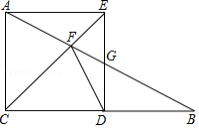
在 中, , .点 在直线 上,以 , 为边作矩形 ,直线 与直线 , 的交点分别为 , .
(1)如图,点 在线段 上,四边形 是正方形.
①若点 为 的中点,求 的长.
②若 ,求 的长.
(2)已知 ,是否存在点 ,使得 是等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由.
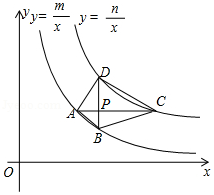
如图,四边形 的四个顶点分别在反比例函数 与 的图象上,对角线 轴,且 于点 .已知点 的横坐标为4.
(1)当 , 时.
①若点 的纵坐标为2,求直线 的函数表达式.
②若点 是 的中点,试判断四边形 的形状,并说明理由.
(2)四边形 能否成为正方形?若能,求此时 , 之间的数量关系;若不能,试说明理由.
如图,抛物线 过点 ,矩形 的边 在线段 上(点 在点 的左边),点 , 在抛物线上.设 ,当 时, .
(1)求抛物线的函数表达式.
(2)当 为何值时,矩形 的周长有最大值?最大值是多少?
(3)保持 时的矩形 不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点 , ,且直线 平分矩形的面积时,求抛物线平移的距离.

如图,在 中,点 在斜边 上,以 为圆心, 为半径作圆,分别与 , 相交于点 , ,连接 .已知 .
(1)求证: 是 的切线.
(2)若 , ,求 的半径.