（年湖南湘西22分）如图，抛物线y=ax2+bx+c关于y轴对称，它的顶点在坐标原点O，点B（2，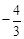
）和点C（﹣3，﹣3）两点均在抛物线上，点F（0，
）在y轴上，过点（0，
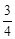）作直线l与x轴平行．
（1）求抛物线的解析式和直线BC的解析式．
（2）设点D（x，y）是线段BC上的一个动点（点D不与B，C重合），过点D作x轴的垂线，与抛物线交于点G．设线段GD的长度为h，求h与x之间的函数关系式，并求出当x为何值时，线段GD的长度h最大，最大长度h的值是多少？
（3）若点P（m，n）是抛物线上位于第三象限的一个动点，连接PF并延长，交抛物线于另一点Q，过点Q作QS⊥l，垂足为点S，过点P作PN⊥l，垂足为点N，试判断△FNS的形状，并说明理由；
（4）若点A（﹣2，t）在线段BC上，点M为抛物线上的一个动点，连接AF，当点M在何位置时，MF+MA的值最小，请直接写出此时点M的坐标与MF+MA的最小值．
如图，在正方形ABCD中，E、F分别是边AD、CD上的点，AE=ED，DF=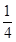
DC，连结
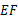并延长交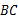
的延长线于点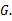
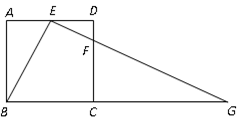
（1）求证：△ABE∽△DEF；
（2）若正方形的边长为4，求BG的长．
已知二次函数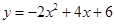
.
（1）求出该函数图象的顶点坐标，图象与x轴的交点坐标．
（2）当x在什么范围内时，y随x的增大而增大？
（3）当x在什么范围内时，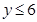
？
已知：正比例函数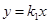
的图象于反比例函数
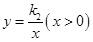的图象交于点M（a，1），MN⊥x轴于点N（如图），若△OMN的面积等于2，求这两个函数的解析式．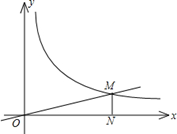
如图，抛物线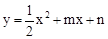
与x轴交于A、B两点，与y轴交于C点，四边形OBHC为矩形，CH的延长线交抛物线于点D（5，2），连结BC、AD.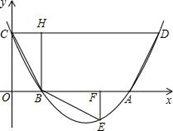
（1）求C点的坐标及抛物线的解析式；
（2）将△BCH绕点B按顺时针旋转90°后再沿x轴对折得到△BEF（点C与点E对应），判断点E是否落在抛物线上，并说明理由；
（3）设过点E的直线交AB边于点P，交CD边于点Q.问是否存在点P，使直线PQ分梯形ABCD的面积为1∶3两部分？若存在，求出P点坐标；若不存在，请说明理由.
如图，一次函数y=kx+n的图象与x轴和y轴分别交于点A（6，0）和B（0，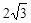
），线段AB的垂直平分线交x轴于点C，交AB于点D.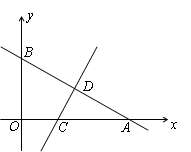
（1）试确定这个一次函数解析式；
（2）求过A、B、C三点的抛物线的函数关系式；
（3）请你利用所求抛物线的图像回答：当x取何值时，抛物线中的部分图像落在x轴的上方？