（年江苏连云港14分）某数学兴趣小组对线段上的动点问题进行探究，已知AB=8.
问题思考：
如图1，点P为线段AB上的一个动点，分别以AP、BP为边在同侧作正方形APDC与正方形PBFE.
（1）在点P运动时，这两个正方形面积之和是定值吗？如果时求出；若不是，求出这两个正方形面积之和的最小值.
（2）分别连接AD、DF、AF，AF交DP于点A，当点P运动时，在△APK、△ADK、△DFK中，是否存在两个面积始终相等的三角形？请说明理由.
问题拓展：
（3）如图2，以AB为边作正方形ABCD，动点P、Q在正方形ABCD的边上运动，且PQ=8.若点P从点A出发，沿A→B→C→D的线路，向D点运动，求点P从A到D的运动过程中，PQ的中点O所经过的路径的长.
（4）如图（3），在“问题思考”中，若点M、N是线段AB上的两点，且AM=BM=1，点G、H分别是边CD、EF的中点.请直接写出点P从M到N的运动过程中，GH的中点O所经过的路径的长及OM+OB的最小值.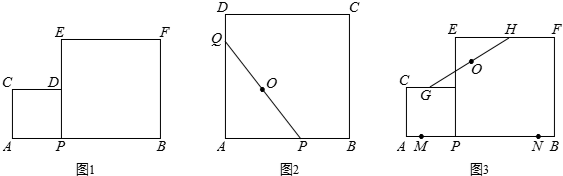
解下列方程：
（1）用配方法解方程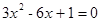
；
（2）用公式法解方程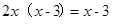
某农户去年承包荒山若干亩，投资7800 元改造后，种果树2000棵．今年水果总产量为18000千克，此水果在市场上每千克售a元，在果园每千克售b元（b＜a）．该农户将水果拉到市场出售平均每天出售1000千克，需8 人帮忙，每人每天付工资25元，农用车运费及其他各项税费平均每天100元．
（1）分别用a，b表示两种方式出售水果的收入?
（2）若a=1．3元，b=1．1元，且两种出售水果方式都在相同的时间内售完全部水果，请你通过计算说明选择哪种出售方式较好．
（3）该农户加强果园管理，力争到明年纯收入达到15000元，那么纯收入增长率是多少? （纯收入=总收入-总支出，该农户采用了（2）中较好的出售方式出售）
为体现社会对教师的尊重，教师节这一天上午，出租车司机小王在东西向的公路上免费接送老师，如果规定向东为正，向西为负，出租车司机的行程如下（单位：千米）：+15，-4，+13，-10，-12，+3，-13，-17．
（1）将最后一名老师送到目的地时，小王距出车地点的距离是多少？
（2）若汽车耗油量为0．4升每千米，这天下午汽车共耗油多少升？
（1）当K为多少时，代数式
（2）关于x的多项式－2x2+mx+nx2－5x－1的值与x的取值无关，求m、n的值．
我们把分子为1的分数叫做单位分数．如
，
，
…，任何一个单位分数都可以拆分成两个不同的单位分数的和，如＝
，＝
，
＝
，…
（1）根据对上述式子的观察，你会发现
．请写出□，○所表示的数；
（2）进一步思考，单位分数
（n是不小于2的正整数）＝
，请写出X、Y所表示的式子．