(2014年山东青岛10分)数学问题:计算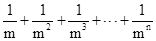 (其中m,n都是正整数,且m≥2,n≥1).
(其中m,n都是正整数,且m≥2,n≥1).
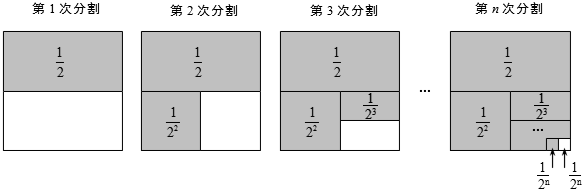
探究问题:为解决上面的数学问题,我们运用数形结合的思想方法,通过不断地分割一个面积为1的正方形,把数量关系和几何图形巧妙地结合起来,并采取一般问题特殊化的策略来进行探究.
探究一:计算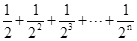 .
.
第1次分割,把正方形的面积二等分,其中阴影部分的面积为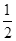 ;
;
第2次分割,把上次分割图中空白部分的面积继续二等分,阴影部分的面积之和为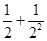 ;
;
第3次分割,把上次分割图中空白部分的面积继续二等分,…;
…
第n次分割,把上次分割图中空白部分的面积最后二等分,所有阴影部分的面积之和为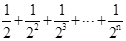 ,最后空白部分的面积是
,最后空白部分的面积是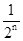 .
.
根据第n次分割图可得等式: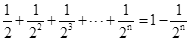 .
.
探究二:计算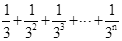 .
.
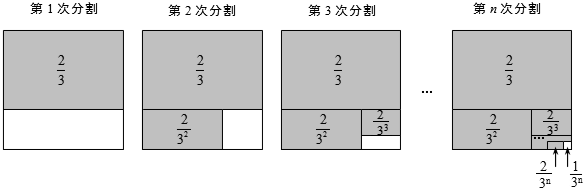
第1次分割,把正方形的面积三等分,其中阴影部分的面积为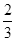 ;
;
第2次分割,把上次分割图中空白部分的面积继续三等分,阴影部分的面积之和为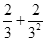 ;
;
第3次分割,把上次分割图中空白部分的面积继续三等分,…;
…
第n次分割,把上次分割图中空白部分的面积最后三等分,所有阴影部分的面积之和为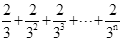 ,最后空白部分的面积是
,最后空白部分的面积是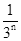 .
.
根据第n次分割图可得等式: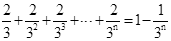 ,
,
两边同除以2,得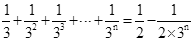 .
.
探究三:计算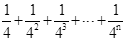 .
.
(仿照上述方法,只画出第n次分割图,在图上标注阴影部分面积,并写出探究过程)

解决问题:计算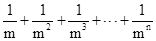 .
.
(只需画出第n次分割图,在图上标注阴影部分面积,并完成以下填空)
根据第n次分割图可得等式: ,
所以,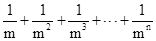 = .
= .
拓广应用:计算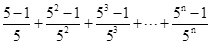 .
.
如图,已知长方形ABCD的长为6,宽为4,请建立适当的平面直角坐标系,分别表示其各个顶点的坐标.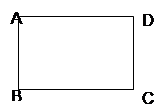
计算题:
(1)
(2)
(3)解方程组
以原点为圆心,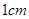 为半径的圆分别交
为半径的圆分别交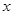 、
、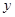 轴的正半轴于A、B两点,点P的坐标为
轴的正半轴于A、B两点,点P的坐标为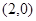 .
.
(1)如图一,动点Q从点B处出发,沿圆周按顺时针方向匀速运动一周,设经过的时间为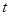 秒,当
秒,当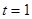 时,直线PQ恰好与⊙O第一次相切,连接OQ.求此时点Q的运动速度(结果保留
时,直线PQ恰好与⊙O第一次相切,连接OQ.求此时点Q的运动速度(结果保留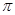 );
);
(2)若点Q按照⑴中的方向和速度继续运动,
①当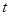 为何值时,以O、P、Q为顶点的三角形是直角三角形;
为何值时,以O、P、Q为顶点的三角形是直角三角形;
②在①的条件下,如果直线PQ与⊙O相交,请求出直线PQ被⊙O所截的弦长.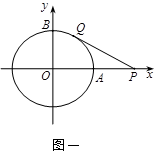
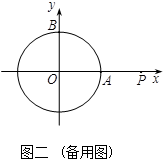
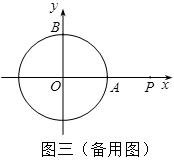
如图1:矩形OABC的顶点A、B在抛物线 上,OC在
上,OC在 轴上,且
轴上,且 .
.
(1)求抛物线的解析式及抛物线的对称轴.
(2)如图2,边长为 的正方形ABCD的边CD在
的正方形ABCD的边CD在 轴上,A、B两点在抛物线上,请用含
轴上,A、B两点在抛物线上,请用含 的代数式表示点B的坐标,并求出正方形边长
的代数式表示点B的坐标,并求出正方形边长 的值.
的值.

我市某工艺品厂生产一款工艺品.已知这款工艺品的生产成本为每件60元.经市场调研发现:该款工艺品每天的销售量y件与售价x元之间存在着如下表所示的一次函数关系.
| 售价x元 |
… |
70 |
90 |
… |
| 销售量y件 |
… |
3000 |
1000 |
… |
(1)求销售量y件与售价x元之间的函数关系式;
(2)设每天获得的利润为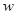 元,当售价x为多少时,每天获得的利润最大?并求出最大值.
元,当售价x为多少时,每天获得的利润最大?并求出最大值.