（年湖北襄阳10分）如图，A，P，B，C是⊙O上的四个点，∠APC=∠BPC=60°，过点A作⊙O的切线交BP的延长线于点D．
（1）求证：△ADP∽△BDA；
（2）试探究线段PA，PB，PC之间的数量关系，并证明你的结论；
（3）若AD=2，PD=1，求线段BC的长．
如图，CD为⊙O的直径，CD⊥AB，垂足为点F，AO⊥BC，垂足为点E，AO=1．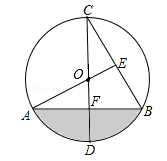
（1）求∠C的大小；
（2）求阴影部分的面积．
先化简，再求值：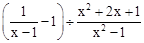
，其中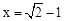
．
如图，在△ABC中，∠C=90°，BC=3，AB=5．点P从点B出发，以每秒1个单位长度沿B→C→A→B的方向运动；点Q从点C出发，以每秒2个单位沿C→A→B方向的运动，到达点B后立即原速返回，若P、Q两点同时运动，相遇后同时停止，设运动时间为t秒．
（1）当t= 时，点P与点Q相遇；
（2）在点P从点B到点C的运动过程中，当ι为何值时，△PCQ为等腰三角形？
（3）在点Q从点B返回点A的运动过程中，设△PCQ的面积为s平方单位．
①求s与ι之间的函数关系式；
②当s最大时，过点P作直线交AB于点D，将△ABC中沿直线PD折叠，使点A落在直线PC上，求折叠后的
△APD与△PCQ重叠部分的面积．
甲、乙两地之间有一条笔直的公路L，小明从甲地出发沿公路ι步行前往乙地，同时小亮从乙地出发沿公路L骑自行车前往甲地，小亮到达甲地停留一段时间，原路原速返回，追上小明后两人一起步行到乙地．设小明与甲地的距离为y1米，小亮与甲地的距离为y2米，小明与小亮之间的距离为s米，小明行走的时间为x分钟．y1、y2与x之间的函数图象如图1，s与x之间的函数图象（部分）如图2．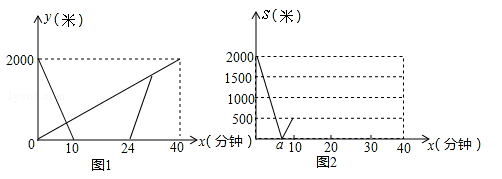
（1）求小亮从乙地到甲地过程中y1（米）与x（分钟）之间的函数关系式；
（2）求小亮从甲地返回到与小明相遇的过程中s（米）与x（分钟）之间的函数关系式；
（3）在图2中，补全整个过程中s（米）与x（分钟）之间的函数图象，并确定a的值．
如图，AB是⊙O的直径，C是⊙0上的一点，直线MN经过点C，过点A作直线MN的垂线，垂足为点D，且∠BAC=∠DAC．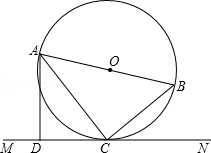
（1）猜想直线MN与⊙O的位置关系，并说明理由；
（2）若CD=6，cos∠ACD=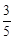
，求⊙O的半径．